Хиральный многогранник (}njgl,udw bukikijguunt)
Существует два определения хирального многогранника. По одному определению — это многогранник в прямом смысле хиральности (или "зеркальной симметричности"), то есть, что многогранник не имеет зеркальной симметрии. По этому определению многогранник, у которого отсутствует любая симметрия, вообще будет примером хирального многогранника.
По другому определению хиральный многогранник — это симметричный многогранник, но не зеркально симметричный в терминах действия группы симметрии многогранника на его флагах. По этому определению даже высокосимметричный и зеркальносимметричный многогранник, такой как плосконосый куб, не будет хиральным. Более того, большая часть изучения симметричных, но не хиральных многогранников, перенесена в область абстрактных многогранников ввиду недостаточности геометрических примеров.
Многогранники без зеркальной симметрии
[править | править код]

|
|
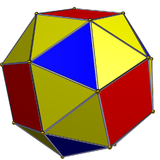
| Плосконосый куб вершинно транзитивен, но не зеркально-симметричен. | |
У многих многогранников отсутствует зеркальная симметрия, и в этом смысле они хиральны. Простейшим примером служит разносторонний треугольник[1].
Многогранник может иметь высокую степень симметрии, но не иметь зеркальной симметрии. Примером служит плосконосый куб, который вершинно транзитивен и хирален ввиду отсутствия зеркальной симметрии[2].
Симметричные хиральные многогранники
[править | править код]Определение
[править | править код]Более формальное определение хирального многогранника — это многогранник, имеющий две орбиты флагов под действием группы симметрии при смежных флагах в различных орбитах. Из этого определения следует, что многогранник должен быть вершинно транзитивен, рёберно транзитивен[англ.] и гране транзитивен, так как каждая вершина, ребро или грань должна быть представлена флагами в обеих орбитах. Однако многогранник не может быть зеркально-симметричен, так как любая зеркальная симметрия многогранника привела бы к обмену смежных флагов[3].
Для этого определения группа симметрии многогранника может быть определена двумя различными путями — она может относиться к симметриям многогранника как геометрического объекта (в этом случае многогранник называется геометрически хиральным) или относиться к симметриям многогранника как комбинаторной структуры (абстрактный многогранник). Хиральность имеет смысл для обоих типов симметрии, но эти два определения не одинаково классифицируют многогранники как хиральные или не хиральные[4].
В трёхмерном пространстве
[править | править код]В трёхмерном пространстве геометрически хиральный многогранник не может иметь конечное число ограниченных граней. Например, плосконосый куб вершинно транзитивен, но его флаги имеют более двух орбит и он ни рёберно-транзитивен, ни гране-транзитивен, так что он недостаточно транзитивен для формального определения хиральности. Квазиправильные многогранники и их двойственные, такие как кубооктаэдр и ромбододекаэдр, дают другой интересный тип «почти отсутствия» — они имеют две орбиты флагов, но зеркально симметричны, и не любая пара смежных флагов принадлежит различным орбитам. Однако, несмотря на отсутствие конечных хиральных трёхмерных многогранников, существуют бесконечные трёхмерные хиральные косые многогранники[англ.] типов {4,6}, {6,4} и {6,6}[4].
Примечания
[править | править код]- ↑ Tilley, 2006, сPA44.
- ↑ Coxeter, 1995, с. 282.
- ↑ Schulte, Weiss, 1991, с. 493–516.
- ↑ 1 2 Schulte, 2004, с. 55–99.
Литература
[править | править код]- Richard J. D. Tilley. Crystals and Crystal Structures. — John Wiley & Sons, 2006. — С. 44. — ISBN 9780470018217.
- H.S.M. Coxeter. Kaleidoscopes: Selected Writings of H. S. M. Coxeter / F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss. — Wiley-Interscience Publication, 1995. — ISBN 978-0-471-01003-6.
- Egon Schulte, Asia Ivić Weiss. Chiral polytopes // Applied Geometry and Discrete Mathematics (The Victor Klee Festschrift) / Gritzmann P., Sturmfels B.. — Providence, RI: American Mathematical Society, 1991. — Т. 4. — С. 493–516. — (DIMACS Series in Discrete Mathematics and Theoretical Computer Science).
- Egon Schulte. Chiral polyhedra in ordinary space. I // Discrete and Computational Geometry. — 2004. — Т. 32, вып. 1. — С. 55–99. — doi:10.1007/s00454-004-0843-x. Архивировано 17 ноября 2010 года.
Литература для дальнейшего чтения
[править | править код]- Barry Monson, Tomaž Pisanski, Egon Schulte, Asia Ivić Weiss. Semisymmetric graphs from polytopes // Journal of Combinatorial Theory. — 2007. — Т. 114, вып. 3. — С. 421–435. — doi:10.1016/j.jcta.2006.06.007..
- Isabel Hubard, Asia Ivićм. Self-duality of chiral polytopes // Journal of Combinatorial Theory. — 2005. — Т. 111, вып. 1. — С. 128–136. — doi:10.1016/j.jcta.2004.11.012.
- Marston Conder, Isabel Hubard, Tomaž Pisanski. Constructions for chiral polytopes // Journal of the London Mathematical Society. — 2008. — Т. 77, вып. 1. — С. 115–129. — doi:10.1112/jlms/jdm093.
- Barry Monson, Asia Ivić Weiss. Cayley graphs and symmetric 4-polytopes // Ars Mathematica Contemporanea. — 2008. — Т. 1, вып. 2. — С. 185–205.
Для улучшения этой статьи желательно:
|