Уравнение Михаэлиса — Ментен (Rjgfuyuny Bn]gzlnvg — Byumyu)

Диаграмма скорости реакции V как функции от концентрации [S].

Уравне́ние Михаэ́лиса — Ме́нтен — уравнение наиболее известной модели ферментативной кинетики, описывает зависимость скорости реакции, катализируемой ферментом, от концентрации субстрата при определённых общепринятых допущениях. Уравнение названо в честь физикохимиков Леонора Михаэлиса и Мод Леоноры Ментен, опубликовавших в 1913 году статью, в которой они провели математический анализ ферментативной кинетики. Простейшая кинетическая схема, для которой справедливо уравнение Михаэлиса:

$E+S\iff ES\longrightarrow E+P$

Уравнение имеет вид:

$v={\frac {V_{m}S}{S+K_{M}}}$,

где

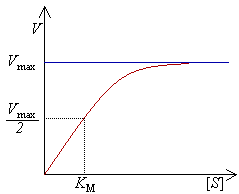
• $V_{m}$ — максимальная скорость реакции, равная $k_{2}E_{0}$;
• $K_{M}$ — константа Михаэлиса. По определению, $K_{M}={\frac {k_{-1}+k_{2}}{k_{1}}}$, где $k_{-1}$ есть константа скорости реакции распада фермент-субстратного комплекса на фермент и исходный субстрат, $k_{1}$ есть константа скорости реакции образования фермент-субстратного комплекса и $k_{2}$ есть константа скорости реакции распада фермент-субстратного комплекса на фермент и продукт (см. ниже вывод уравнения для скорости реакции). Константа Михаэлиса численно равна концентрации субстрата, при которой скорость реакции составляет половину от максимальной;
• $S$ — концентрация субстрата.

Вывод уравнения

Вывод уравнения был впервые предложен Бриггсом и Холдейном. Вывод уравнения скорости ферментативной реакции, описываемой схемой Михаэлиса — Ментен.

Обозначения констант скоростей:

$k_{1}$ — константа скорости реакции образования фермент-субстратного комплекса из фермента и субстрата

$k_{-1}$ — константа скорости реакции диссоциации фермент-субстратного комплекса на фермент и субстрат

$k_{2}$ — константа скорости реакции превращения фермент-субстратного комплекса в фермент и продукт

Для фермент-субстратного комплекса применим метод квазистационарности, так как в подавляющем большинстве реакций константа скорости превращения фермент-субстратного комплекса в фермент и продукт много больше, чем константа скорости образования ферменто-субстратного комплекса из фермента и субстрата. Иными словами:

${\frac {d[ES]}{dt}}=k_{1}[E][S]-(k_{-1}+k_{2})[ES]=0$

Учтем тот факт, что фермент, изначально находившийся только в свободной форме, в процессе реакции находится как в виде фермент-субстратного комплекса, так и в виде молекул свободного фермента. Таким образом:

$[E]_{0}=[E]+[ES]$

Преобразуем это к виду:

$[E]=[E]_{0}-[ES]$

И подставим в первое уравнение. После раскрытия скобок и группировки слагаемых получим следующее:

${\frac {d[ES]}{dt}}=k_{1}[E]_{0}[S]-(k_{1}[S]+k_{-1}+k_{2})[ES]=0$

Выразим отсюда концентрацию фермент-субстратного комплекса:

$[ES]={\frac {k_{1}[E]_{0}[S]}{k_{1}[S]+k_{-1}+k_{2}}}$

Скорость ферментативной реакции в целом (то есть скорость образования продукта) представляет собой скорость распада фермент-субстратного комплекса по реакции первого порядка с константой k₂:

$v=k_{2}[ES]$

Подставим в эту формулу выражение, которое мы получили для концентрации ES. Получим:

$v={\frac {k_{1}k_{2}[E]_{0}[S]}{k_{1}[S]+k_{-1}+k_{2}}}$

Разделим числитель и знаменатель на k₁. В результате:

$v={\frac {k_{2}[E]_{0}[S]}{{\frac {k_{-1}+k_{2}}{k_{1}}}+[S]}}$

Выражение в знаменателе — (k₋₁+k₂)/k₁ — называется константой Михаэлиса (K_m). Это кинетическая константа (с размерностью концентрации), которая равняется такой концентрации субстрата, при которой скорость ферментативной реакции составляет половину от максимального значения.

Для начальной стадии реакции можно пренебречь уменьшением концентрации субстрата. Тогда выражение для начальной скорости реакции будет выглядеть так:

$v_{0}={\frac {k_{2}[E]_{0}[S]_{0}}{[S]_{0}+K_{m}}}$

Если k₋₁>>k₂, то на первой стадии ферментативной реакции с течением времени устанавливается равновесие (квазиравновесный режим протекания реакции), и в выражение для скорости ферментативной реакции входит уже не константа Михаэлиса, а субстратная константа K_S, характеризующая взаимодействие фермента с субстратом в равновесных условиях:

$v_{0}={\frac {v_{max}[S]}{[S]+K_{s}}}$; $K_{s}={\frac {k_{-1}}{k_{1}}}={\frac {[E][S]}{[ES]}}$

По значению K_S можно судить о химическом сродстве субстрата к ферменту.

См. также

• Ферментативная кинетика