Теорема Тебо (Mykjybg MyQk)

Теорема Тебо — три теоремы планиметрии, приписываемые Тебо.

Первая теорема Тебо

Центры квадратов, построенных на сторонах параллелограмма, лежат в вершинах квадрата.

Эта теорема является частным случаем теоремы Ван-Обеля и аналогична теореме Наполеона.

Вторая теорема Тебо

Если на каждой из двух соседних сторон квадрата построить по равностороннему треугольнику (либо оба внутрь, либо оба вовне квадрата), то вершины этих 2 треугольников, не являющиеся вершинами квадрата, и вершина квадрата, не являющаяся вершиной треугольников, образуют равносторонний треугольник.

Третья теорема Тебо

Доказана в 1930-х годах.

Теорема Тебо

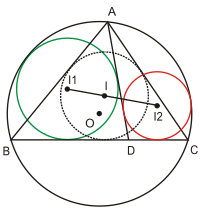
Пусть $ABC$ — произвольный треугольник, $D$ — произвольная точка на стороне $BC$, $I_{1}$ — центр окружности, касающейся отрезков $AD,BD$ и описанной около $\Delta ABC$ окружности, $I_{2}$ — центр окружности, касающейся отрезков $CD,AD$ и описанной около $\Delta ABC$ окружности. Тогда отрезок $I_{1}I_{2}$ проходит через точку $I$ — центр окружности, вписанной в $\Delta ABC$, и при этом $I_{1}I:II_{2}=\operatorname {tg} ^{2}{\frac {\varphi }{2}}$, где $\varphi =\angle BDA$.

Вариация третьей теоремы Тебо

Теорема. Если во вписанном в окружность четырёхугольнике провести диагональ, а в полученные два треугольника вписать две окружности, затем аналогично поступить, проведя вторую диагональ, тогда центры четырёх образовавшихся окружностей являются вершинами прямоугольника.

См. также

• Теорема Ван-Обеля о четырёхугольнике
• Теорема Наполеона

Литература

• Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 341—343. — 383 с. — ISBN 5-09-001287-3.