Теорема Паппа (Mykjybg Hghhg)

Теорема Паппа

Теоре́ма Па́ппа — это классическая теорема проективной геометрии.

Формулировка

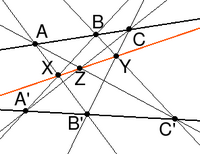
Пусть A, B, C — три точки на одной прямой, A' , B' , C'  — три точки на другой прямой. Пусть три прямые АВ' , BC' , CA' пересекают три прямые A’B, B’C, C’A, соответственно в точках X, Y, Z. Тогда точки X, Y, Z лежат на одной прямой.

Замечания

Двойственная формулировка к теореме Паппа является лишь переформулировкой самой теоремы:

Пусть прямые $a_{1},a_{2},a_{3}$ проходят через точку A, $a_{1}',a_{2}',a_{3}'$ проходят через точку A'. $a_{1}$ пересекает $a_{2}'$ и $a_{3}'$ в точках B и C, $a_{2}$ пересекает $a_{1}'$ и $a_{3}'$ в точках C' и Z, $a_{3}$ пересекает $a_{1}'$ и $a_{2}'$ в точках B' и X. Тогда прямые BC', B’C и XZ пересекаются в одной точке (на чертеже — точка Y) или параллельны.

История

Формулировка и доказательство этой теоремы содержатся в «Математическом собрании» Паппа Александрийского (начало IV века н. э.). В Новое время теорема была опубликована издателем и комментатором работ Паппа Федерико Коммандино в 1566 году.

Доказательства

Точки X, Y, Z лежат на одной прямой

Доказательство удалением точек на бесконечность

Пусть точка $O$ — точка пересечения прямых, на которых лежат точки $A$, $B$, $C$ и $A'$, $B'$, $C'$.

Рассмотрим пересечения прямых:

$AB'\cap A'B=X$

$AC'\cap A'C=Y$

$CB'\cap C'B=Z$

Теперь применим проективное отображение, переводящее прямую $XY$ на бесконечность.

Так как $X=\infty$: $AB'\parallel A'B$, $Y=\infty$: $AC'\parallel A'C$. Теперь необходимо доказать, что $BC'\parallel B'C$.

Рассмотрим подобные треугольники.

$\bigtriangleup OAC'\sim \ \bigtriangleup OCA'\Rightarrow {\frac {OC}{OA'}}={\frac {OA}{OC'}}\Rightarrow OA\cdot OA'=OC\cdot OC'$

$\bigtriangleup OAB'\sim \ \bigtriangleup OBA'\Rightarrow {\frac {OB}{OA'}}={\frac {OA}{OB'}}\Rightarrow OA\cdot OA'=OB\cdot OB'$

Отсюда следует, что ${\frac {OB}{OC}}={\frac {OB'}{OC'}}\Rightarrow \bigtriangleup OCB'\sim \bigtriangleup OBC'$ (по второму признаку подобия треугольников) $\Rightarrow BC'\parallel B'C$.

Что и требовалось доказать.

Доказательство через теорему Менелая

Применяя к треугольникам $\bigtriangleup AXB$, $\bigtriangleup AYC$ и $\bigtriangleup BZC$ теорему Менелая, также можно доказать данное утверждение.

Вариации и обобщения

Теорема Паппа является вырожденным случаем в теореме Паскаля: если заменить в теореме Паскаля вписанный в конику шестиугольник на вписанный в пару пересекающихся прямых, то она станет эквивалентной теореме Паппа. Сам Паскаль считал пару прямых коническим сечением (то есть считал теорему Паппа частным случаем своей теоремы).

Двойственная формулировка является вырожденным случаем Теоремы Брианшона.

См. также

• Теорема Паппа о площадях

Литература

• Р.Курант, Г.Роббинс, Что такое математика? Глава IV, § 5.3.