Супер-крестики-нолики (Vrhyj-tjyvmntn-uklntn)
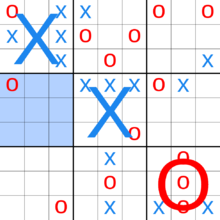

Супер-крестики-нолики (ультимативные крестики-нолики, мега-крестики-нолики, крестики-нолики в квадрате) — настольная игра, состоящая из поля размером 9×9 клеток, разделённого на девять досок для игры в крестики-нолики. По сравнению с традиционными крестиками-ноликами, стратегия в этой игре концептуально сложнее и оказалась более сложной для компьютеров[1].
Правила
[править | править код]В супер-крестики-нолики играют 2 игрока. Один из них ставит на поле крестики, а другой — нолики.
Каждое маленькое поле (3×3) называется малой доской, а большое (9×9) — глобальной доской.
Первыми ходят крестики. Они могут сыграть в любую из 81 клетки. Своим ходом они «отправляют» нолики на одну из малых досок. Например, если крестики сходили в правый нижний угол малого поля, нолики должны сделать ход на правой нижней доске, в свою очередь, «отправляя» крестики на одно из полей.
Если ход сделан так, что он должен выиграть малую доску по правилам обычных крестиков-ноликов, она отмечается соответствующим знаком (X или O) как победа игрока. Как только малое поле выиграно игроком или полностью заполнено, на нем больше не может быть сделано ни одного хода. Если игрок отправлен на такую доску, то он может играть на любой другой доске.
Игра заканчивается, когда либо игрок выигрывает глобальную доску, либо не остаётся ни одного законного хода; в этом случае побеждает тот игрок, который победил на большем количестве малых досок (при одинаковом количестве объявляется ничья).
Альтернативные правила
[править | править код]Другая версия игры позволяет игрокам продолжать игру на уже выигранных досках, если там ещё есть свободные места. Это позволяет игре длиться дольше и включает в неё дополнительные стратегические ходы. В 2020 году было показано, что этот набор правил допускает выигрышную стратегию для первого игрока (крестиков), что означает, что он всегда может выиграть при условии идеальной игры.[2] Если игра с этим набором правил все ещё предпочтительна, проблема вынужденного выигрыша может быть практически решена путем случайной генерации первых 4 ходов.[3]
Игровой процесс
[править | править код]Супер-крестики-нолики значительно сложнее, чем большинство других разновидностей крестиков-ноликов, поскольку в них нет чёткой стратегии игры. Это происходит из-за сложного игрового разветвления в этой игре. Несмотря на то, что каждый ход должен быть сыгран на малом поле, эквивалентном обычной доске для игры в крестики-нолики, он должен учитывать глобальную доску несколькими способами.
Предвидение следующего хода: каждый ход, сделанный на локальной доске, определяет, куда может быть сделан следующий ход противника. Это может сделать ходы, которые в обычных крестиках-ноликах считаются плохими, жизнеспособными, поскольку противник отправляется на другое поле и не может немедленно отреагировать на них. Таким образом, игроки вынуждены рассматривать глобальную доску, вместо того чтобы просто сосредоточиться на малых полях.
Визуализация дерева игры: представление будущих ветвей дерева игры намного сложнее, чем в оригинальных крестиках-ноликах. Каждый ход определяет следующий ход, и поэтому чтение вперёд — предсказание будущих ходов — идёт по гораздо менее линейному пути. Будущие ходы на доске больше не взаимозаменяемы, каждый ход приводит к разительно отличающимся позициям. Это делает дерево игры трудным для визуализации.
Победа в игре: в соответствии с правилами игры, глобальная доска никогда не подвергается прямому воздействию. Она управляется только действиями, происходящими на малых полях. Это означает, что каждый ход делается в основном не для победы на малой доске, а для победы на глобальном поле. Местные победы почти не имеют ценности, если они не могут быть использованы для победы на глобальной сетке — стратегически может быть выгодно пожертвовать доску противнику, чтобы самому выиграть более важное поле. Эта дополнительная сложность затрудняет анализ относительной важности и значимости ходов, и, следовательно, затрудняет хорошую игру.
Компьютерные реализации
[править | править код]В то время как «крестики-нолики» элементарно решаются[4] и могут быть сделаны почти мгновенно с помощью поиска в глубину, супер-крестики-нолики не могут быть разумно решены с помощью грубой силы. Поэтому для игры в эту игру необходимы более творческие компьютерные реализации.
Тактика «минимакс» может быть использована для игры в супер-крестики-нолики, но при этом возникают трудности. Это связано с тем, что, несмотря на относительно простые правила, в конечной тактике отсутствует простая эвристическая функция оценки. Эта функция необходима в минимаксе, поскольку она определяет, насколько хороша та или иная позиция. Хотя для супер-крестиков-ноликов можно сделать элементарные оценочные функции, принимая во внимание количество локальных побед, они в значительной степени упускают из виду позиционное преимущество, которое гораздо труднее оценить количественно. Без какой-либо эффективной функции оценки большинство типичных компьютерных реализаций слабы, и поэтому существует мало компьютерных противников, которые могут последовательно обыгрывать людей[1].
Однако алгоритмы искусственного интеллекта, которым не нужны функции оценки, такие как алгоритм поиска по дереву Монте-Карло, без проблем играют в эту игру. Поиск по дереву Монте-Карло опирается на случайное моделирование игр для определения того, насколько хороша позиция, вместо позиционной оценки и поэтому способен точно оценить, насколько хороша текущая позиция. Поэтому компьютерные реализации, использующие эти алгоритмы, как правило, превосходят минимаксные решения и могут последовательно побеждать человеческих оппонентов.[5][6]
Варианты
[править | править код]Тик-Так-Ку — игра, придуманная Марком Асперхаймом и Крисом Ван Оостерумом[7][8] Правила игры такие же, как и в супер-крестиках-ноликах, единственное исключение — игрок побеждает, выиграв как минимум пять малых досок.
Примечания
[править | править код]- ↑ 1 2 Wayback Machine. web.archive.org (29 июля 2021). Дата обращения: 11 июня 2023. Архивировано 29 июля 2021 года.
- ↑ Computer Science. arxiv.org. Дата обращения: 11 июня 2023. Архивировано 14 декабря 2022 года.
- ↑ Mathematics. arxiv.org. Дата обращения: 11 июня 2023. Архивировано 19 апреля 2023 года.
- ↑ MathRec Solutions (Tic-Tac-Toe). web.archive.org (24 февраля 2020). Дата обращения: 11 июня 2023. Архивировано из оригинала 24 февраля 2020 года.
- ↑ Mathematics. arxiv.org. Дата обращения: 11 июня 2023. Архивировано 22 декабря 2017 года.
- ↑ What is the Monte Carlo tree search? blog.theofekfoundation.org. Дата обращения: 11 июня 2023. Архивировано 11 июня 2023 года.
- ↑ 2009年度门萨最佳动脑奖揭晓 - 桌游世界_(桌面游戏网)_最权威、娱乐的中文桌游门户网及在线桌面游戏平台. www.173zy.com. Дата обращения: 11 июня 2023. Архивировано 4 марта 2016 года.
- ↑ Tic Tac Ku - Marbles: The Brain Store. web.archive.org (10 июня 2012). Дата обращения: 11 июня 2023. Архивировано 10 июня 2012 года.