Сжатый граф (V'gmdw ijgs)

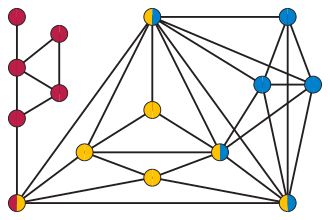
Сжатый граф, образованный как сумма по клике, используемая для склеивания вместе максимального планарного графа (жёлтого) и двух хордальных графов (красного и синего). Красный хордальный граф может быть, в свою очередь, разложен на суммы по кликам четырёх максимальных планарных графов (два ребра и два треугольника).

Сжатый граф — граф, в котором удаление рёбер любого порождённого цикла с длиной, большей трёх, даёт несвязный граф. То есть это графы, в которых каждый периферийный цикл является треугольником.

Примеры

В максимальном планарном графе, или более обще, в любом полиэдральном графе, периферийные циклы в точности грани планарного вложения графа, так что полиэдральный граф сжат тогда и только тогда, когда все грани являются треугольниками, или, эквивалентно, он является максимально планарным. Любой хордальный граф является сжатым, поскольку лишь порождённые циклы в хордальных графах являются треугольниками, так что нет больше циклов для удаления.

Описание

Сумма по клике двух графов образуется путём отождествления двух клик одинакового размера в каждом графе, а затем часть рёбер клики удаляется. Для версии сумм по клике для сжатых графов шаг удаления рёбер опускается. Сумма по клике такого типа двух сжатых графов приводит к другому сжатому графу, в котором любой длинный порождённый цикл в сумме должен быть ограничен одной стороной или другой (в противном случае была бы хорда между вершинами, которая проходит от одной стороны суммы в другую), а несвязные части на этой стороне, образованные путём удаления цикла, должны остаться несвязными в сумме по клике. Любой хордальный граф может быть разложен таким образом на сумму по клике полных графов, и любой максимальный планарный граф может быть разложен на сумму по клике вершинно 4-связного графа максимальных планарных графов.

Как показали Сеймур и Вивер, это единственно возможные строительные блоки для сжатых графов — сжатые графы, это в точности графы, которые могут быть образованы как суммы по клике полных графов и максимальных планарных графов.

См. также

• Рёберно совершенный граф, в котором любой нечётный цикл является треугольником