Прошитое двоичное дерево (Hjkonmky ;fkncuky ;yjyfk)

Прошитое двоичное дерево — это вариант двоичного дерева, который позволяет производить быстрый обход — если дан указатель на узел в прошитом дереве, можно легко найти следующий по порядку узел (и/или предыдущий).
Предпосылки
[править | править код]Двоичные деревья, включая двоичные деревья поиска (но не ограничиваясь ими) и их варианты, могут быть использованы для сохранения множества элементов в определённом порядке. Например, двоичное дерево поиска предполагает, что элементы данных упорядочены каким-либо образом и сохраняют этот порядок при вставке и удалении. Одна полезная операция над таким деревом — обход, то есть посещение элементов дерева в порядке, в котором они будут запомнены (который соответствует упорядочению узлов в случае дерева двоичного поиска).
Алгоритм простого рекурсивного обхода, который посещает каждый узел дерева двоичного поиска, следующий. Предположим, что t — указатель на узел или nil. «Посещение» t может означать любую операцию с этим узлом t или приписанным ему содержимым.
Алгоритм обхода(t):
- Вход: указатель t на узел (или nil)
- Если t = nil, возврат.
- Иначе:
- Обходим(левый-предок(t))
- Посещаем t
- Обходим (правый-предок(t))
Проблема этого алгоритма заключается в том, что ввиду рекурсии алгоритм использует пространство стека, пропорциональное высоте дерева. Если дерево достаточно сбалансировано, эта величина достигает O(log n) для дерева из n элементов. В наихудшем случае, когда дерево принимает форму цепочки, высота дерева равна n, так что алгоритм потребует пространство стека величиной O(n).
В 1968, Дональд Кнут задал вопрос, существует ли нерекурсивный алгоритм центрированного обхода, который не использует стек и оставляет дерево неизменным. Одно из решений этой проблемы — прошивка дерева, представленная Джеймсом Х. Моррисом в 1979[1][2].
Определение
[править | править код]Прошитое дерево определяется следующим образом:
«Двоичное дерево прошивается путём присвоения всем указателям правого потомка, которые обычно были бы нулевыми указателями, указателей на следующий по порядку узел данного узла (если такой существует), а всем указателям левого потомка, которые обычно были бы нулевыми указателями, указателей на предыдущие узлы в упорядочении»[3].
Можно также найти родителя узла из прошитого двоичного дерева без явного использования указателя на родителя или стека, хотя медленнее. Это полезно, когда стек имеет ограничение, или когда стек указателей на родителей недоступен (для нахождения указателя на родителя с помощью поиска в глубину).
Чтобы понять, как это возможно, рассмотрим узел k, имеющий правого потомка r. Тогда левый указатель узла r должен быть либо потомком, либо указателем обратно на k. В случае, когда r имеет левого потомка, то левый потомок должен иметь своего левого потомка, либо указатель назад к k, и так далее для всех последующих левых потомков. Таким образом, перебирая последовательно цепочку левых указателей из r, мы, в конце концов, находим прошивочный указатель обратно на k. Ситуация симметрична, когда q является левым потомком p, в этом случае мы можем проследовать правые потомки узла q для получения прошивочного указателя на p.
Типы прошитых двоичных деревьев
[править | править код]- Одиночное прошивание: каждый узел прошивается указателем либо на предыдущий по порядку узел, либо на следующий по порядку узел (левый или правый).
- Двойное прошивание: каждый узел прошивается указателем как на предыдущий узел, так и на следующий (левый и правый).
На языке Python:
def parent(node):
if node is node.tree.root:
return None
else:
x = node
y = node
while True:
if is_thread(y):
p = y.right
if p is None or p.left is not node:
p = x
while not is_thread(p.left):
p = p.left
p = p.left
return p
elif is_thread(x):
p = x.left
if p is None or p.right is not node:
p = y
while not is_thread(p.right):
p = p.right
p = p.right
return p
x = x.left
y = y.right
Массив центрированного обхода
[править | править код]Прошивка — это ссылки на предшествующий и последующий узлы данного узла согласно центрированному обходу.
Если порядок прошитого дерева — это ABCDEFGHI, узел D предшествует E, а F следует за узлом E.
Пример
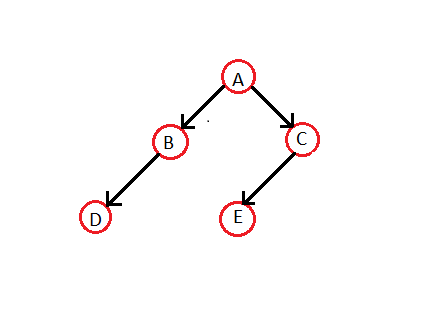
[править | править код]Попытаемся сформировать прошитое дерево из обычного двоичного дерева
Упорядочение вершин центрированного обхода для дерева выше — D B A E C. Таким образом, соответствующее прошитое двоичное дерево будет выглядеть следующим образом
Нулевой указатель
[править | править код]В прошитом m-кратно двоичном дереве с n узлами, существует n*m — (n-1) пустых ссылок.
Нерекурсивный центрированный обход для прошитого двоичного дерева
[править | править код]Как нерекурсивный метод обхода, метод должен быть итеративной процедурой, все шаги обхода узла должны быть в цикле, так что то же самое можно применить ко всем узлам дерева. Мы снова предположим центрированный обход дерева. Тогда для любого узла мы обходим сначала левое поддерево (если оно существует и в случае, если мы не обходили его ранее). Затем мы посещаем (то есть печатаем значение узлов в нашем случае) сам узел, а уж затем обходим правое поддерево (если оно существует). Если правого дерева нет, проверяем прошитую ссылку и делаем прошитую вершину текущим узлом в рассмотрении. Смотрите пример ниже.
Алгоритм
[править | править код]Шаг-1: Для текущего узла проверяем, имеется ли левый потомок, которого нет в списке посещённых. Если такой имеется, переходим к шагу 2, иначе — к шагу 3.
Шаг-2: Помещаем левого потомка в список посещённых узлов и делаем его текущим узлом. Переходим к шагу 6.
Шаг-3: Печатаем узел и если узел имеет правого потомка, переходим к шагу 4, иначе переходим к шагу 5.
Шаг-4: Делаем правого потомка текущим узлом.
Шаг-5: Если существует прошивочный узел, делаем его текущим узлом.
Шаг-6: Если все узлы напечатаны, завершаем работу, иначе переходим к шагу 1.
| Список | ||||
|---|---|---|---|---|
| шаг-1 | A имеет левого потомка то есть B, который ещё не посещён, так что помещаем B в наш «список посещённых узлов» и B становится текущим узлом. | B | ||
| шаг-2 | B также имеет левого потомка D, которого нет в списке посещённых узлов. Помещаем D в список посещённых и делаем текущим. | B D | ||
| шаг-3 | У узла D нет левого потомка, так что печатаем D, затем проверяем правого потомка. D не имеет правого потомка, так что смотрим на прошитую ссылку. Узел имеет прошивку к узлу B, так что делаем B текущим. | B D | D | |
| шаг-4 | B имеет левого потомка, но он уже посещён. Таким образом, печатаем B, затем проверяем на наличие правого потомка, но его нет, так что мы делаем прошитый узел (то есть A) текущим. | B D | D B | |
| шаг-5 | A имеет левого потомка B, но он уже посещён, так что печатаем A и проверяем наличие правого потомка. Узел A имеет правого потомка C и он отсутствует в списке посещённых узлов, так что мы добавляем его в этот список и делаем текущим. | B D C | D B A | |
| шаг-6 | C имеет узел E в качестве левого потомка и этот узел ещё не посещён, так что добавляем узел E в список и делаем его текущим. | B D C E | D B A | |
| шаг-7 | наконец….. | D B A E C |
Примечания
[править | править код]- ↑ Morris, 1979.
- ↑ Mateti, Manghirmalani, 1988, с. 29–43.
- ↑ Van Wyk, 1988, с. 175.
Литература
[править | править код]- Joseph H. Morris. Traversing binary trees simply and cheaply // Information Processing Letters. — 1979. — Т. 9, вып. 5. — doi:10.1016/0020-0190(79)90068-1.
- Prabhaker Mateti, Ravi Manghirmalani. Morris' tree traversal algorithm reconsidered // Science of Computer Programming. — 1988. — Т. 11. — С. 29–43. — doi:10.1016/0167-6423(88)90063-9.
- Christopher J. Van Wyk. Data Structures and C Programs. — Addison-Wesley, 1988. — С. 175. — ISBN 978-0-201-16116-8.
Ссылки
[править | править код]Для улучшения этой статьи желательно:
|