Произведение графов (Hjkn[fy;yuny ijgskf)

Произведение графов — это бинарная операция на графах. Конкретнее, это операция, которая двум графам G₁ и G₂ сопоставляет граф H со следующими свойствами:

• Множество вершин графа H — это прямое произведение V(G₁) × V(G₂), где V(G₁) и V(G₂) являются множествами вершин G₁ и G₂ соответственно.
• Две вершины (u₁, u₂) и (v₁, v₂) графа H соединены ребром тогда и только тогда, когда вершины u₁, u₂, v₁, v₂ удовлетворяют определённым условиям, соответствующим типу произведения (смотрите ниже).

Виды произведений

Следующая таблица показывает наиболее употребительные произведения графов. В таблице $\sim$ означает «соединены ребром» и $\not \sim$ означает «не соединены ребром». Символы операций, приведённые ниже, не всегда означают стандарт, особенно в ранних работах.

Название	Условие для ($u_{1}$, $u_{2}$) ∼ ($v_{1}$, $v_{2}$).	Размеры	Пример
Декартово произведение $G\square H$	( $u_{1}$ = $v_{1}$ и $u_{2}$ $\sim$ $v_{2}$ ) или ( $u_{1}$ $\sim$ $v_{1}$ и $u_{2}$ = $v_{2}$ )	$G_{V_{1},E_{1}}\square H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(E_{2}V_{1}+E_{1}V_{2})}$
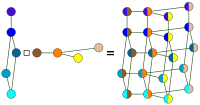
Тензорное произведение (Категорийное произведение) $G\times H$	$u_{1}$ $\sim$ $v_{1}$ и $u_{2}$ $\sim$ $v_{2}$	$G_{V_{1},E_{1}}\times H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(2E_{1}E_{2})}$
Лексикографическое произведение $G\cdot H$ или $G[H]$	u1 ∼ v1 или ( u1 = v1 и u2 ∼ v2 )	$G_{V_{1},E_{1}}\cdot H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(E_{2}V_{1}+E_{1}V_{2}^{2})}$
Сильное произведение (Нормальное произведение) $G\boxtimes H$	( u1 = v1 и u2 ∼ v2 ) или ( u1 ∼ v1 и u2 = v2 ) или ( u1 ∼ v1 и u2 ∼ v2 )	$G_{V_{1},E_{1}}\boxtimes H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(V_{1}E_{2}+V_{2}E_{1}+2E_{1}E_{2})}$
Конормальное произведение графов (Дизъюнктное произведение) $G*H$	u1 ∼ v1 или u2 ∼ v2
Модулярное произведение	$(u_{1}\sim v_{1}$ и $u_{2}\sim v_{2})$ или $(u_{1}\not \sim v_{1}$ и $u_{2}\not \sim v_{2})$
Корневое произведение	см. статью	$G_{V_{1},E_{1}}\cdot H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(E_{2}V_{1}+E_{1})}$
Произведение Кронекера	см. статью	см. статью	см. статью
Зигзаг-произведение	см. статью	см. статью	см. статью
Заменяющее произведение
Гомоморфное произведение $G\ltimes H$	$(u_{1}=v_{1})$ или $(u_{1}\sim v_{1}$ и $u_{2}\not \sim v_{2})$

В общем случае произведение графов определяется любым условием для (u₁, u₂) ∼ (v₁, v₂), которое может быть выражено в терминах утверждений u₁ ∼ v₁, u₂ ∼ v₂, u₁ = v₁ и u₂ = v₂.

Мнемоника

Пусть $K_{2}$ — полный граф с двумя вершинами (т.е. единственное ребро). Произведения графов $K_{2}\square K_{2}$, $K_{2}\times K_{2}$, и $K_{2}\boxtimes K_{2}$ выглядят в точности как знак операции умножения. Например, $K_{2}\square K_{2}$ является циклом длины 4 (квадрат), а $K_{2}\boxtimes K_{2}$ является полным графом с четырьмя вершинами. Нотация $G[H]$ для лексикографического произведения напоминает, что произведение не коммутативно.

См. также

• Операции над графами