Правило Тициуса — Боде (Hjgfnlk Mnenrvg — >k;y)

Правило Тициуса — Боде
Правило Тициуса — Боде
Названо в честь	Тициус, Иоганн Даниэль и Иоганн Элерт Боде
Шкала измерения	астрономическая единица
	Медиафайлы на Викискладе

Правило Ти́циуса — Бо́де (называемое также законом Бо́де) представляет собой эмпирическую формулу, приблизительно описывающую расстояния между планетами Солнечной системы и Солнцем (средние радиусы орбит). Эта закономерность была обнаружена Иоганном Тициусом в 1766 году и получила известность благодаря работам Иоганна Боде в 1772 году.

Правило устанавливает, что начиная с Меркурия каждая следующая планета располагается примерно вдвое дальше от Солнца, чем предыдущая. Наблюдения показали, что первые семь планет (если учесть и малые планеты пояса астероидов как возможные обломки пятой планеты) с хорошей точностью следуют этому правилу; открытый в 1781 году Уран также хорошо вписался в общую закономерность. Однако Нептун выпадает из правила. Строгого теоретического обоснования данной математической закономерности до сих пор не существует. Делаются попытки обобщить правило на спутники планет➤ и на известные экзопланеты➤.

Формулировка

Правило формулируется следующим образом.

К каждому элементу последовательности $D_{i}=0,3,6,12,\dots$ прибавляется 4, затем результат делится на 10. Полученное число считается радиусом орбиты i-й планеты в астрономических единицах. То есть,

R_{i}={\frac {D_{i}+4}{10}}.

Последовательность $D_{i}$ — геометрическая прогрессия, кроме первого числа. То есть, $D_{-1}=0;D_{i}=3\cdot 2^{i},i\geqslant 0$ .

Эту же формулу можно записать по-другому:

R_{-1}=0{,}4,

R_{i}=0{,}4+0{,}3\cdot 2^{i}.

Встречается также другая формулировка:

Для любой планеты среднее расстояние от её орбиты до орбиты самой внутренней планеты (в Солнечной системе — Меркурия) в два раза больше, чем среднее расстояние от орбиты предыдущей планеты до орбиты самой внутренней планеты:

{R_{i}-R_{\text{☿}}}=2\cdot (R_{i-1}-R_{\text{☿}}).

Результаты вычислений приведены в таблице^[1] (где $k_{i}=D_{i}/3=0,1,2,4,...$ ). Видно, что этой закономерности соответствует и пояс астероидов, а Нептун, напротив, из закономерности выпадает, причём его место занимает Плутон, хотя он, согласно решению XXVI Ассамблеи МАС исключён из числа планет.

Планета	$i$	$k_{i}$	Радиус орбиты (а.е.)		${\frac {R_{i}-R_{\text{☿}}}{R_{i-1}-R_{\text{☿}}}}$
Планета	$i$	$k_{i}$	по правилу	фактический	${\frac {R_{i}-R_{\text{☿}}}{R_{i-1}-R_{\text{☿}}}}$
Меркурий	$-\infty$	0	0,4	0,39
Венера	0	1	0,7	0,72
Земля	1	2	1,0	1,00	1,825
Марс	2	4	1,6	1,52	1,855
Пояс астероидов	3	8	2,8	в сред. 2,2—3,6	2,096 (по орбите Цереры)
Юпитер	4	16	5,2	5,20	2,021
Сатурн	5	32	10,0	9,54	1,9
Уран	6	64	19,6	19,22	2,053
Нептун	выпадает			30,06	1,579
Плутон	7	128	38,8	39,5	2,078 (по отношению к Урану)
Эрида	8	256	77,2	67,7

История

Первое упоминание о подобной закономерности встречается в учебнике Дэвида Грегори «Начала астрономии» (The Elements of Astronomy, 1715):

…предположим, что расстояние Земли от Солнца разделено на десять равных частей, из которых расстояние от Меркурия будет примерно четыре, от Венеры семь, от Марса пятнадцать, от Юпитера пятьдесят два, а от Сатурна девяносто. пять.

Когда в 1766 году Тициус впервые строго сформулировал это правило (в приложении к своему переводу работы Шарля Бонне), ему удовлетворяли все известные в то время планеты (от Меркурия до Сатурна), имелся лишь пропуск на месте пятой планеты. В 1772 году Боде в своём «Путеводителе по знанию звездного неба» (Anleitung zur Kenntniß des gestirnten Himmels) Боде изложил (без упоминания Тициуса) то же правило; впоследствии Боде признал приоритет Тициуса.

Новый закон не привлёк большого внимания до тех пор, пока в 1781 году не был открыт Уран, который почти точно лёг на предсказанную последовательность. После этого Боде призвал начать поиски недостающей планеты между Марсом и Юпитером. Именно в том месте, где должна была располагаться эта планета, была обнаружена Церера. Это вызвало рост доверия к правилу Тициуса — Боде среди астрономов, которое сохранялось до открытия Нептуна. Когда выяснилось, что, кроме Цереры, примерно на том же расстоянии от Солнца находится множество тел, формирующих пояс астероидов, была выдвинута гипотеза, что они образовались в результате разрушения планеты (Фаэтона), которая раньше находилась на этой орбите.

Попытки обоснования

Правило не имеет конкретного математического и аналитического (через формулы) объяснения, основанного только на теории гравитации, так как не существует общих решений так называемой «задачи трёх тел» (в простейшем случае), или «задачи N тел» (в общем случае). Прямое численное моделирование также затруднено огромным объёмом вычислений.

Одно из вероятных объяснений правила заключается в следующем. Уже на стадии формирования Солнечной системы в результате гравитационных возмущений, вызванных протопланетами и их резонансом с Солнцем (при этом возникают приливные силы, и энергия вращения тратится на приливное ускорение или, скорее, замедление), сформировалась регулярная структура из чередующихся областей, в которых могли или не могли существовать стабильные орбиты согласно правилам орбитальных резонансов (то есть отношение радиусов орбит соседних планет равных 1/2, 3/2, 5/2, 3/7 и т. п.)^[2]. Впрочем, часть астрофизиков полагает, что это правило — всего лишь случайное совпадение.

Резонансным орбитам сейчас в основном соответствуют планеты или группы астероидов, которые постепенно (за десятки и сотни миллионов лет) выходили на эти орбиты. В случаях, когда планеты (а также астероиды и планетоиды за Плутоном) не расположены на стабильных орбитах (как Нептун) и не расположены в плоскости эклиптики (как Плутон), наверняка в ближайшем (относительно сотен миллионов лет) прошлом имели место инциденты, нарушавшие их орбиты (столкновение, близкий пролёт массивного внешнего тела). Со временем (быстрее к центру системы и медленнее на окраинах системы) они неизбежно займут стабильные орбиты, если им не помешают новые инциденты.

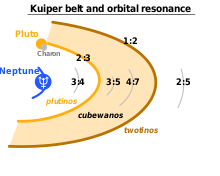
Наличие стабильных орбит, вызванных резонансами между телами системы, впервые численно смоделировано (компьютерная симуляция движения точечных взаимодействующих масс вокруг резонирующего центра — Солнца, представленного как две точечные массы с упругой связью) и приведено в сравнении с реальными астрономическими данными в работах 1998—1999 годов профессора Рену Малхотра.^{[источник не указан 3687 дней]}

Само существование резонансных орбит и само явление орбитального резонанса в нашей планетной системе подтверждается экспериментальными данными по распределению астероидов по радиусу орбиты и плотности объектов KBO пояса Койпера по радиусу их орбиты.

Сравнивая структуру стабильных орбит планет Солнечной системы с электронными оболочками простейшего атома, можно обнаружить некоторое подобие, хотя в атоме переход электрона происходит практически мгновенно только между стабильными орбитами (электронными оболочками), а в планетарной системе выход небесного тела на стабильные орбиты занимает десятки и сотни миллионов лет.

Проверка для спутников планет Солнечной системы

Три планеты Солнечной системы — Юпитер, Сатурн и Уран — имеют систему спутников, которые, скорее всего, сформировались в результате таких же процессов, как и в случае самих планет. Эти системы спутников образуют регулярные структуры, на основе орбитальных резонансов, которые, правда, не подчиняются правилу Тициуса — Боде в его первоначальном виде. Однако, как выяснил в 1960-е годы астроном Стэнли Дермотт (англ. Stanley Dermott), можно немного обобщить правило Тициуса — Боде:

T(n)=T(0)\cdot C^{n},\quad n=1,2,3,4\ldots ,

где $T$ — орбитальный период (дней). Оценку точности правила Дермотта^[англ.] для системы спутников Юпитера, Сатурна и Урана представляют следующие таблицы^[3]:

Юпитер: T(0) = 0,444, C = 2,03

Спутник		n	Результат расчёта	Фактически
Jupiter V	Амальтея	1	0,9013	0,4982
Jupiter I	Ио	2	1,8296	1,7691
Jupiter II	Европа	3	3,7142	3,5512
Jupiter III	Ганимед	4	7,5399	7,1546
Jupiter IV	Каллисто	5	15,306	16,689
Jupiter VI	Гималия	9	259,92	249,72

Сатурн: T(0) = 0,462, C = 1,59

Спутник		n	Результат расчёта	Фактически
Saturn I	Мимас	1	0,7345	0,9424
Saturn II	Энцелад	2	1,1680	1,3702
Saturn III	Тетис	3	1,8571	1,8878
Saturn IV	Диона	4	2,9528	2,7369
Saturn V	Рея	5	4,6949	4,5175
Saturn VI	Титан	7 8	11,869 18,872	15,945
Saturn VIII	Япет	11	75,859	79,330

Уран: T(0) = 0,488, C = 2,24

Спутник		n	Результат расчёта	Фактически
Uranus V	Миранда	1	1,0931	1,4135
Uranus I	Ариэль	2	2,4485	2,5204
Uranus II	Умбриэль	3	5,4848	4,1442
Uranus IV	Оберон	4	13,463	12,286

Проверка для экзопланет

Тимоти Боверд (англ. Timothy Bovaird) и Чарльз Лайнвивер (Charles H. Lineweaver) из Австралийского национального университета проверили^[4] применимость правила к экзопланетным системам (2013 год). Из известных систем, содержащих по четыре открытых планеты, они отобрали 27 таких, для которых добавление дополнительных планет между известными нарушало бы стабильность системы. Считая отобранные кандидаты полными системами, авторы показали, что для них выполняется обобщённое правило Тициуса — Боде, аналогичное предложенному Дермоттом:

R_{i}=R\cdot C^{i},\quad i=0,1,2,3,...,

где R и C — параметры, обеспечивающие наилучшее приближение к наблюдаемому распределению.

Было обнаружено, что из 27 отобранных для анализа систем 22 системы удовлетворяют взаимным соотношениям радиусов орбит даже лучше, чем Солнечная система, 2 системы подходят под правило примерно как Солнечная, у 3 систем правило работает хуже Солнечной.

Для 64 систем, которые по выбранному критерию не были полными, авторы попытались предсказать орбиты ещё не открытых планет. Всего ими сделано 62 предсказания с помощью интерполяции (в 25 системах) и 64 — с помощью экстраполяции. Оценка максимальных масс планет, сделанная по чувствительности приборов, с помощью которых были открыты эти системы экзопланет, показывает, что некоторые из предсказанных планет должны быть земного типа. Согласно проверке Chelsea X. Huang и Gáspár Á. Bakos (2014), фактически обнаруживаемое количество планет на таких орбитах существенно ниже предсказанного и, таким образом, использование соотношения Тициуса — Боде для заполнения «недостающих» орбит — под вопросом^[5]: на предсказываемых орбитах планеты образуются не всегда. Тем не менее пять планет на предсказанных орбитах были впоследствии обнаружены. Например, была предсказана неизвестная планета в звёздной системе KOI 2722; два месяца спустя эта экзопланета была обнаружена с помощью космического телескопа «Кеплер»^[6].

Согласно уточнённой проверке M. B. Altaie, Zahraa Yousef, A. I. Al-Sharif (2016 г.), для 43 экзопланетных систем, содержащих четыре или более планеты, соотношение Тициуса — Боде выполняется с высокой точностью при условии изменения масштабов радиусов орбит. Исследование также подтверждает масштабную инвариантность закона Тициуса — Боде^[7]^{[неавторитетный источник]}.

Современные статистические данные (2020 год) по экзопланетным орбитам убедительно указывают на общее выполнение законов, подобных Тициусу – Боде (то есть экспоненциального увеличения больших полуосей в зависимости от номера планеты) во всех экзопланетных системах и для всех известных систем экзопланет, для которых известна величины полуосей^[8]^[9],

Проблемы теории

Правило Тициуса — Боде входит в некоторое противоречие с моделью Ниццы. Модель описывает формирование Солнечной системы с учётом миграции планет и предполагает, что они не всегда занимали современное положение. Следовательно, должны были существовать периоды (по меньшей мере переходные), когда положение планет не укладывалось в уравнение^{[источник не указан 2651 день]}.

Примечания

↑ Александр Березин. Новости науки Архивная копия от 6 августа 2018 на Wayback Machine.
↑ Правило Тициуса—Боде (неопр.). Дата обращения: 12 января 2011. Архивировано 25 августа 2011 года.
↑ Dermott, S. F. (1969). "On the origin of commensurabilities in the solar system - III: The resonant structure of the solar system". Mon. Not. R. Astron. Soc. 142 (2): 143—149. Bibcode:1969MNRAS.142..143D. doi:10.1093/mnras/142.2.143.
↑ Timothy Bovaird, Charles H. Lineweaver. Exoplanet Predictions Based on the Generalised Titius-Bode Relation Архивная копия от 9 августа 2020 на Wayback Machine.
↑ [https://web.archive.org/web/20200809153632/https://arxiv.org/abs/1405.2259 Архивная копия от 9 августа 2020 на Wayback Machine [1405.2259] Testing the Titius-Bode law predictions for Kepler multi-planet systems].
↑ Guido Meyer (2014). Planetenformel – irrer Zufall oder Naturgesetz? Архивная копия от 11 декабря 2022 на Wayback Machine
↑ M. B. Altaie, Zahraa Yousef, A. I. Al-Sharif. Applying Titius-Bode’s Law on Exoplanetry Systems Архивная копия от 6 августа 2020 на Wayback Machine.
↑ Lara, Patricia; Cordero-Tercero, Guadalupe; Allen, Christine (2020). "The reliability of the Titius–Bode relation and its implications for the search for exoplanets". Publications of the Astronomical Society of Japan. 72 (2). arXiv:2003.05121. doi:10.1093/pasj/psz146.
↑ Ballesteros, F. J.; Fernandez-Soto, A.; Martinez, V.J. (2019). "Title: Diving into Exoplanets: Are Water Seas the Most Common?". Astrobiology. 19 (5): 642—654. doi:10.1089/ast.2017.1720. hdl:10261/213115. PMID 30789285. S2CID 73498809.

Литература

Ньето М. Закон Тициуса — Боде. История и теория. М.: Мир, 1976.
Планетарные орбиты и протон. «Наука и жизнь» № 1, 1993. С. 155.
Hahn, J. M., Malhotra, R. Orbital evolution of planets embedded in a massive planetesimal disk, AJ 117:3041—3053 (1999)
Malhotra, R. Migrating Planets, Scientific American 281(3):56—63 (1999)
Malhotra, R. Chaotic planet formation, Nature 402:599—600 (1999)
Malhotra, R. Orbital resonances and chaos in the Solar system, in Solar System Formation and Evolution, Rio de Janeiro, Brazil, ASP Conference Series vol. 149 (1998). Preprint
Showman, A., Malhotra, R. The Galilean Satellites, Science 286:77 (1999)

Ссылки

Правило XVIII века в большинстве планетарных систем выполняется лучше, чем в Солнечной Архивная копия от 14 апреля 2013 на Wayback Machine
Malhotra’s research spans orbital dynamics in the solar system and in extra-solar planetary systems (недоступная ссылка) (англ.)
Анимация графики распределения астероидов по орбитам Архивная копия от 29 мая 2014 на Wayback Machine (англ.)

[1] Александр Березин. Новости науки Архивная копия от 6 августа 2018 на Wayback Machine.

[Природа_науки-2] Правило Тициуса—Боде (неопр.). Дата обращения: 12 января 2011. Архивировано 25 августа 2011 года.

[3] Dermott, S. F. (1969). "On the origin of commensurabilities in the solar system - III: The resonant structure of the solar system". Mon. Not. R. Astron. Soc. 142 (2): 143—149. Bibcode:1969MNRAS.142..143D. doi:10.1093/mnras/142.2.143.

[4] Timothy Bovaird, Charles H. Lineweaver. Exoplanet Predictions Based on the Generalised Titius-Bode Relation Архивная копия от 9 августа 2020 на Wayback Machine.

[5] [https://web.archive.org/web/20200809153632/https://arxiv.org/abs/1405.2259 Архивная копия от 9 августа 2020 на Wayback Machine [1405.2259] Testing the Titius-Bode law predictions for Kepler multi-planet systems].

[6] Guido Meyer (2014). Planetenformel – irrer Zufall oder Naturgesetz? Архивная копия от 11 декабря 2022 на Wayback Machine

[7] M. B. Altaie, Zahraa Yousef, A. I. Al-Sharif. Applying Titius-Bode’s Law on Exoplanetry Systems Архивная копия от 6 августа 2020 на Wayback Machine.

[8] Lara, Patricia; Cordero-Tercero, Guadalupe; Allen, Christine (2020). "The reliability of the Titius–Bode relation and its implications for the search for exoplanets". Publications of the Astronomical Society of Japan. 72 (2). arXiv:2003.05121. doi:10.1093/pasj/psz146.

[9] Ballesteros, F. J.; Fernandez-Soto, A.; Martinez, V.J. (2019). "Title: Diving into Exoplanets: Are Water Seas the Most Common?". Astrobiology. 19 (5): 642—654. doi:10.1089/ast.2017.1720. hdl:10261/213115. PMID 30789285. S2CID 73498809.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]