Популяционная модель (Hkhrlxenkuugx bk;yl,)

Популяционная модель — математическая модель, применяемая для изучения динамики численности популяции.

Обоснование

Модели позволяют лучше понять, как протекают процессы со сложными взаимодействиями. Моделирование динамических взаимодействий в природе может обеспечить управляемый способ понимания того, как числа меняются со временем или по отношению друг к другу. Многие закономерности можно заметить, используя моделирование популяции^[1].

При экологическом моделировании популяции определяют динамику изменения размер популяции (численности особей) и распределение их по возрастам. Это может зависеть от взаимодействия с окружающей средой, особями того же и других видов^[2].

Популяционные модели используют агрономы для определения максимального урожая, для понимания динамики биологических инвазий и для охраны окружающей среды. Популяционные модели также используются для понимания распространения паразитов, вирусов и болезней^[2].

Еще один способ использования моделей популяций — это оценка находится ли биологический вид на грани опасности исчезновения. Модели популяции могут отслеживать исчезающие виды и предлагать меры сдерживания сокращения их численности [1] Архивная копия от 28 июля 2018 на Wayback Machine.

История

В конце XVIII века биологи начали разрабатывать методы моделирования популяций, чтобы понять динамику роста и сокращения всех популяций живых организмов. Томас Мальтус одним из первых заметил, что население росло в геометрической прогрессии^[3], хотя неявно это было сделано уже Фибоначчи. Одной из основных моделей роста населения была логистическая модель роста населения, сформулированная Пьером Франсуа Ферхульстом в 1838 году. Логистическая модель принимает форму сигмовидной кривой и описывает рост населения как экспоненциальный с замедлением роста из-за давления окружающей среды^[1].

Моделирование популяций стало особенно интересным для биологов в XX веке, после того как биолог Рэймонд Перл, заметил влияние ограниченных средств к существованию на увеличение численности населения в некоторых частях Европы. В 1921 году Перл пригласил физика Альфреда Лотку помочь ему в его лаборатории. Лотка разработал парные дифференциальные уравнения, которые показали влияние хищника на его добычу. Математик Вито Вольтерра предложил уравнения описывающие взаимоотношения между двумя видами (хищник и добыча) независимо от Лотки. Вместе Лотка и Вольтерра сформулировали модель конкуренции Лотки — Вольтерры, которая применяет логистическое уравнение к двум видам, и иллюстрирует взаимодействие в системе двух видов хищник-добыча^[3]. В 1939 году Патрик Лесли внёс вклад в моделирование популяций, когда он начал работать в области биоматематики. Лесли подчеркнул важность составления таблицы жизни, чтобы понять влияние ключевых стратегий жизненной истории на динамику населения в целом. Лесли применил матричную алгебру в сочетании с таблицами жизни, чтобы расширить работу Лотки^[4]. Матричные модели популяции рассчитывают рост численности с переменными истории жизни. Позднее Роберт Макартур и Э.О. Уилсон создали островную биогеографию. Равновесная модель островной биогеографии описывает количество видов на острове как равновесие иммиграции и вымирания. Логистическая популяционная модель, модель экологии сообщества Лотки – Вольтерры, моделирование матрицы жизненных таблиц, равновесная модель островной биогеографии и её вариации являются основой современного экологического моделирования популяций^[5].

Уравнения

Уравнение логистического роста :

{\frac {dN}{dt}}=rN\left(1-{\frac {N}{K}}\right)\,

Уравнение Лотки — Вольтерры:

{\frac {dN_{1}}{dt}}=r_{1}N_{1}{\frac {K_{1}-N_{1}-\alpha N_{2}}{K_{1}}}\,

Островная биогеография :

S={\frac {IP}{I+E}}

Видовые отношения :

\log(S)=\log(c)+z\log(A)\,

Примеры индивидуальных моделей

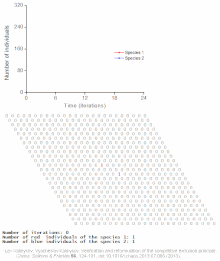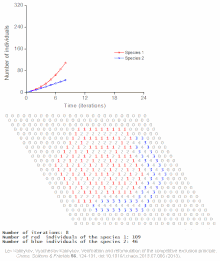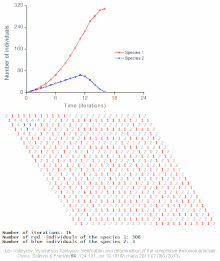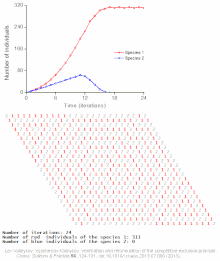
Ва-Тор (Wa-Tor)

См. также

Динамика населения
Популяционная динамика рыболовства
Экология населения
Момент закрытия

Примечания

↑ ¹ ² Worster, Donald. Nature's Economy (неопр.). — Cambridge University Press, 1994. — С. 398—401.
↑ ¹ ² Uyenoyama, Marcy. The Evolution of Population Biology (неопр.). — Cambridge University Press, 2004. — С. 1—19.
↑ ¹ ² McIntosh, Robert. The Background of Ecology (неопр.). — Cambridge University Press, 1985. — С. 171—198.
↑ Kingsland, Sharon. Modeling Nature: Episodes in the History of Population Ecology (англ.). — University of Chicago Press, 1995. — P. 127—146.
↑ Gotelli, Nicholas. A Primer of Ecology (неопр.). — Sinauer^[англ.], 2001.

Ссылки

Сеть обмена кодами GreenBoxes . Greenboxes (бета-версия) является хранилищем кода моделирования популяций с открытым исходным кодом. Greenboxes позволяет пользователям легко делиться своим кодом и искать другой общий код.

[Worster-1] ¹ ² Worster, Donald. Nature's Economy (неопр.). — Cambridge University Press, 1994. — С. 398—401.

[Uyenoyama-2] ¹ ² Uyenoyama, Marcy. The Evolution of Population Biology (неопр.). — Cambridge University Press, 2004. — С. 1—19.

[McIntosh-3] ¹ ² McIntosh, Robert. The Background of Ecology (неопр.). — Cambridge University Press, 1985. — С. 171—198.

[4] Kingsland, Sharon. Modeling Nature: Episodes in the History of Population Ecology (англ.). — University of Chicago Press, 1995. — P. 127—146.

[5] Gotelli, Nicholas. A Primer of Ecology (неопр.). — Sinauer^[англ.], 2001.

[1]

[2]

[3]

[4]

[5]