Полярный момент инерции (Hklxjudw bkbyum nuyjenn)

Не следует путать с Момент инерции.

Схема к вычислению полярного момента инерции

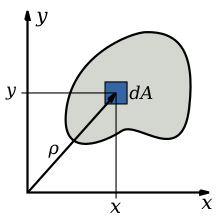
Поля́рный моме́нт ине́рции — интегральная сумма произведений площадей, элементарных площадок dA на квадрат их расстояния от полюса — ρ², взятого по всей площади сечения. То есть:

$J_{p0}=\int _{A}\rho ^{2}\,dA$

Эта величина используется для прогнозирования способности объекта оказывать сопротивление кручению. Она имеет размерность единиц длины в четвёртой степени (м⁴, см⁴) и может быть лишь положительной.

Для площади сечения, имеющей форму круга радиусом r полярный момент инерции равен:

$J_{p0}=\int _{0}^{2\pi }\int _{0}^{r}\rho ^{2}\rho \,d\rho \,d\phi ={\frac {\pi r^{4}}{2}}={\frac {\pi (D/2)^{4}}{2}}={\frac {\pi D^{4}}{32}}.$

Если совместить начало декартовой прямоугольной системы координат 0 с полюсом полярной системы (см. рис.), то:

$J_{p0}=J_{x}+J_{y}$

потому что $\rho ^{2}=x^{2}+y^{2}.$

Применение

Полярный момент инерции используется в формулах, которые описывают зависимость между касательными напряжениями и крутящим моментом, который их вызывает. Касательное напряжение:

$\tau ={\frac {Tr}{J_{p0}}}$

где

$T$ — крутящий момент,

$r$ — расстояние от оси кручения

${J_{p0}}$ — полярный момент инерции.

Полярный момент инерции для некоторых случаев

Распределение касательных напряжений при кручении

Для круглого сплошного сечения:

$J_{p0}={\frac {\pi D^{4}}{32}}$

где $D$ — диаметр круга.

Для кольцевого сечения (полый вал):

$J_{p0}={\frac {\pi D^{4}}{32}}\left(1-{\frac {d^{4}}{D^{4}}}\right),$

где $D$ — внешний диаметр кольца,

$d$ — внутренний диаметр кольца.

См. также

• Полярный момент сопротивления
• Момент инерции

Литература

• Феодосьев В. И. Сопротивление материалов. Изд. 10-е, перераб. и доп. - М.: МГТУ им. Н. Э. Баумана, 1999 год. Рецензенты академик РАН Образцов И. Ф. и д. т. н профессор Чирков И. П.