Оптимизация неоднородности (Khmnbn[genx uyk;ukjk;ukvmn)

Оптимизация неоднородности (англ. Discontinuity layout optimization, DLO) — метод определения величины нагрузки, которую может выдержать конструкция до разрушения. Предполагается, что разрушение происходит пластическим образом.
Как это устроено
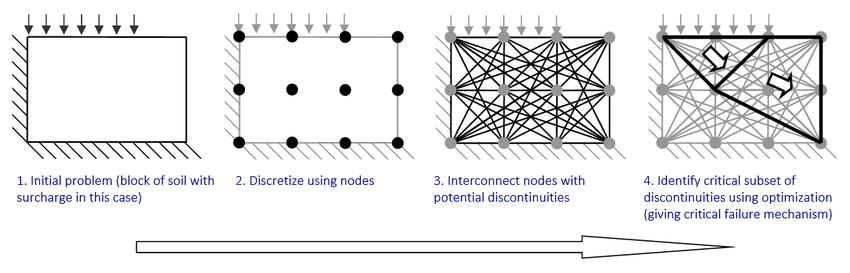
[править | править код]Оптимизация неоднородности включает ряд шагов, описанных ниже.
Набор потенциальных неоднородностей может включать в себя неоднородности, которые пересекаются друг с другом, что позволяет идентифицировать сложные модели отказов (например, с участием «веерных» механизмов, когда из одной точки исходит множество неоднородностей).
Оптимизация неоднородности можно сформулировать в терминах отношений равновесия («статическая» формулировка) или в терминах перемещений («кинематическая» формулировка). В последнем случае целью задачи математической оптимизации является минимизация внутренней энергии, рассеиваемой вдоль разрывов, с учетом узловых ограничений совместимости. Эту проблему можно решить с помощью эффективных методов линейного программирования, и в сочетании с алгоритмом, изначально разработанным для задач оптимизации компоновки ферм, [1] было обнаружено, что современные компьютерные мощности можно использовать для прямого поиска в очень большом количестве различных топологий механизмов разрушения. (примерно до 2 1 000 000 000 различных топологий на ПК текущего поколения). Полное описание применения DLO к задачам о плоской деформации было предоставлено Смитом и Гилбертом [2], к анализу каменной арки Гилбертом и др., [3] к задачам плиты Гилбертом и др., [4] [5] [6] и трехмерным задачам Hawksbee et al, [7] и Zhang. [8]
Оптимизация неоднородности против Метода конечных элементов
[править | править код]В то время как при анализе методом конечных элементов (МКЭ), широко используемой альтернативной процедуре инженерного анализа, математические отношения формируются для основной проблемы механики сплошной среды, Оптимизация неоднородности включает анализ потенциально гораздо более простой проблемы неоднородности, при этом проблема ставится полностью с точки зрения отдельных разрывы, соединяющие между собой узлы, расположенные поперек рассматриваемого тела. Кроме того, когда для анализа состояния коллапса используются программы конечных элементов общего назначения, часто требуются относительно сложные нелинейные решатели, в отличие от более простых решателей линейного программирования, которые обычно требуются в случае DLO.
По сравнению с нелинейным МКЭ, Оптимизация неоднородности имеет следующие преимущества и недостатки:
Преимущества
- Состояние коллапса анализируется напрямую, без необходимости повторения. Это означает, что решения, как правило, могут быть получены гораздо быстрее.
- Выходные данные в виде анимированных механизмов отказа, как правило, легче интерпретировать.
- Проблемы, связанные с сингулярностями в полях напряжений или перемещений, решаются без труда.
- Поскольку Оптимизация неоднородностинамного проще, чем нелинейный FEM, пользователям требуется меньше обучения, чтобы эффективно использовать этот метод.
Недостатки
- Как и другие методы предельного анализа, Оптимизация неоднородности не предоставляет информации о смещениях (или напряжениях) до обрушения.
- DLO в основном основан на моделировании совместимых механизмов обрушения почвы и, следовательно, является методом верхней границы . В результате метод всегда будет предсказывать неконсервативную разрушающую нагрузку.
- Хотя генерация схемы разрыва и схемы оптимизации линейного программирования, используемые в DLO, обычно гарантируют, что будет найдено хорошее приближение к истинному механизму обрушения, нет никакого способа определить, насколько прогнозируемая нагрузка обрушения превысит истинную нагрузку обрушения без сравнения с независимый анализ нижней границы .
- DLO — относительно новый метод, поэтому в настоящее время доступен лишь ограниченный набор программных инструментов.
Приложения
[править | править код]Оптимизация неоднородности наиболее полезно применять к инженерным задачам, где традиционные ручные вычисления сложны, но где обращение к более сложным нелинейным МКЭ не оправдано. Приложения включают в себя:
- Анализ инженерно -геологических проблем (например, устойчивость откосов, несущая способность [9] или проблемы с подпорными стенками ).
- Анализ проблем бетонной плиты .
- Анализ проблем штамповки или экструзии металла.
Программное обеспечение, использующее оптимизацию макета разрыва797
[править | править код]- Скрипт MATLAB (2009-) Предоставлен исследовательской группой CMD Университета Шеффилда, Великобритания.
- LimitState:GEO (2008-) Геотехническое программное приложение общего назначения.
- LimitState:SLAB (2015-) Программное приложение для анализа плит.
Примечания
[править | править код]- ↑ Gilbert, M. and Tyas, A. (2003) Layout optimization of large-scale pin-jointed frames, Engineering Computations, Vol. 20, No. 8, pp.1044-1064
- ↑ Smith, C.C. and Gilbert, M. (2007) Application of discontinuity layout optimization to plane plasticity problems, Proc. Royal Society A, Volume 463, Number 2086, pp.2461-2484.
- ↑ Gilbert, M., Smith, C.C. and Pritchard, T.J. (2010) Masonry arch analysis using discontinuity layout optimisation. ICE-Engineering and Computational Mechanics, Volume 163, pp.167-178.
- ↑ Gilbert, M., He, L., Smith, C.C. and Le, C.V. (2014) Automatic yield-line analysis of slabs using discontinuity layout optimization. Proceedings Royal Society A, Volume 470, paper 20140071.
- ↑ He, L., Gilbert, M. and Shepherd, M. (2017) Automatic yield-line analysis of practical slab configurations via discontinuity layout optimization. Journal of Structural Engineering, DOI:10.1061/(ASCE)ST.1943-541X.0001700
- ↑ He, L. and Gilbert, M. (2016) Automatic rationalization of yield-line patterns identified using discontinuity layout optimization. International Journal of Solids and Structures, Volume 84, pp.27-39.
- ↑ Hawksbee, S., Smith, C.C. and Gilbert, M. (2013) Application of discontinuity layout optimization to three-dimensional plasticity problems. Proceedings Royal Society A, Volume 469, paper 20130009.
- ↑ Zhang, Y. (2017) Multi-slicing strategy for the three-dimensional discontinuity layout optimization (3D DLO). International Journal for Numerical and Analytical Methods in Geomechanics, Volume 41, pp.488-507.
- ↑ Lee, Y.S., Smith C.C. and Cheuk C.Y. (2008) Bearing capacity of embedded foundations. In 2nd International Conference on Foundations, ICOF 2008, Dundee, pp.961-972.