Обменное смещение (KQbyuuky vbypyuny)

Кривые перемагничивания в направлении лёгкой оси:
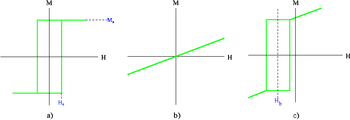
a) магнитно мягкого материала;
b) высокоанизотропного антиферромагнетика (магнитная восприимчивость преувеличена);
c) магнитного материала с эффектом обменного смещения.

Обме́нное смеще́ние (или: обме́нная анизотропи́я, анизотропи́я обме́нного взаимоде́йствия, однонапра́вленная анизотропи́я обме́на) — особенность петель гистерезиса перемагничивания магнитных материалов, проявляющаяся в несимметричном расположении петли относительно оси ординат. Наблюдается в слоистых и наноструктурных магнитных материалах, содержащих магнитно мягкую ферромагнитную и высокоанизотропную антиферромагнитную фазу.

Природа эффекта

Смещение петли гистерезиса в слоистых материалах, как правило, объясняется тем, что магнитно мягкая компонента испытывает влияние одной из магнитных подрешёток антиферромагнитной компоненты. Такое влияние называется обменным подмагничиванием или пиннингом.

История открытия

Эффект обменного смещения, известный также как однонаправленная анизотропия, был обнаружен в 1956 г. Мейклджоном и Бином при изучении частиц кобальта, внедренных в антиферромагнитный оксид CoO . С самого начала был сделан вывод о том, что смещение петли гистерезиса вызвано наличием слоя оксида, окружающего частицы кобальта. Это означало, что магнитное взаимодействие через их общий интерфейс имеет определяющее значение в создании эффекта. После того, как его признали исключительно интерфейсным явлением, обменное смещение стало исследоваться в основном на тонких пленках, состоящих из контактирующих ферромагнитного (ФМ) и антиферромагнитного (АФМ) слоев. В настоящее время, однако, вновь стали активно изучаться литографически приготовленные структуры, а также ферромагнитные и антиферромагнитные частицы.

Основные модели эффекта

Первой и самой простой моделью, призванной объяснить эффект, стала теория, предложенная Мейклджоном и Бином. В своей работе они исследовали однодоменные сферические частицы кобальта, покрытые оболочкой из антиферромагнитного CoO. Эти частицы обладали одноосной анизотропией, и их ось легкого намагничивания (ОЛН) выстраивалась параллельно приложенному магнитному полю. Они предположили, что спиновая конфигурация антиферромагнетика на интерфейсе совершенно не скомпенсирована и остается выровненной вдоль её ОЛН благодаря значительной анизотропии АФМ и более слабой обменной связи между антиферромагнетиком и ферромагнетиком. Такой механизм обменного смещения приводит к сдвигу петли гистерезиса на величину H_ex, которая на два порядка выше, чем величины, наблюдаемые в мелкозеренных поликристаллических пленках, хотя данная теория неплохо описывает другие системы.

Хронологически второй моделью, объясняющей эффект обменного смещения, является теория Нееля. Неель предложил модель некомпенсированной спиновой структуры АФМ на интерфейсе. Однако он указывал на то, что эта спиновая структура подвержена деформации и испытывает необратимые изменения во время разворота намагниченности ФМ слоя. Следовательно, поле обменного смещения H_ex и коэрцитивная сила H_с определяются изменениями в АФМ в ходе перемагничивания ферромагнитного слоя. Согласно его теории, H_с имеет два вклада: внутренняя ферромагнитная компонента и член, который будет пропорционален необратимым изменениям намагниченности в АФМ. Также Неель рассматривал то, что для реальных шероховатых интерфейсов обе подрешетки антиферромагнетика должны быть представлены в области интерфейса, что приводит к частичной компенсации АФМ моментов. В случае поликристаллических АФМ число спинов на интерфейсе каждого зерна антиферромагнетика может иметь статистическое распределение, что ведет к флуктуациям моментов каждого зерна АФМ. Данная теория также не подходит для расчета значений H_ex.

Наиболее успешной теорией обменного смещения можно считать модель Фалкомера и Кэрэпа. Ученые провели как экспериментальное, так и теоретическое исследования обменного смещения в пленках пермаллоя, в которых в ходе обработки кислотным паром постепенно окислялся никель с образованием изолированных зерен АФМ на поверхности пленки. Они наблюдали в таких системах прогрессирующие изменения обменного смещения, связанные как с ростом размера зерна, так и с увеличением количества зерен АФМ материала. Количественное моделирование, основанное на модели разворота гранул, аналогичной системе Стонера–Вольфарта, имеет хорошее согласие с экспериментальными наблюдениями. В частности, Фалкомер и Кэрэп прогнозировали, что обменное поле, действующее на АФМ ферромагнетиком, может привести к термически активированным изменениям ориентации подрешеток АФМ, что, в свою очередь, ведет к изменению значения H_ex. Важной особенностью данной теории является то, что были рассмотрены случаи с большим разбросом по размеру и форме зерен АФМ. Таким образом, значения энергий анизотропии и обменной связи варьировались в широком диапазоне. Распределение по размеру зерен было принято таким, чтобы все значения были равновероятны до некоторого максимума, а зерен большего размера не было. Они обнаружили важность рассмотрения распределения по размеру зерен, но форма такого распределения не являлась критичной. Данная модель была способна предсказать температурные зависимости величин H_ex и H_с в широком диапазоне температур, включая области выше температуры Нееля, как сообщается в. В целом, эта теория стала базой для других моделей гранул (зерен), основанных на эффектах тепловых флуктуаций.

К числу более современных теорий магнитного обменного смещения можно отнести модели Маури, Малоземова, Стайлза и Мак’Майкла, Стэмпса, Новака и др. Одна из теорий температурного поведения величины обменного смещения была предложена О’Грейди в 2009 году.

Несмотря на то, что эффект обменного смещения был открыт в середине двадцатого столетия, до сих пор нет окончательной теории, которая могла бы объяснить сдвиг петли гистерезиса (H_ex) и увеличенное значение коэрцитивной силы (H_c) (определяемое как половина ширины петли). Одной из причин, почему не была разработана ясная и всеобъемлющая теория, является то, что изученный на сегодняшний день круг образцов отличается большим разнообразием. К таким образцам относятся наночастицы, где, очевидно, интерфейс АФМ/ФМ не является плоским, эпитаксиально выращенные пленки, интерфейс в которых почти идеально плосок, и напыленные поликристаллические пленки, где интерфейс имеет значительную шероховатость, что может привести как к структурному, так и к магнитному беспорядку. Интересно отметить, что наибольшее обменное смещение при комнатной температуре наблюдается в поликристаллических (гранулированных) пленках, полученных распылением, и именно эти материалы используются для применения в таких устройствах, как магнитные записывающие головки и приложения MRAM.