Независимое множество (Uy[gfnvnbky buk'yvmfk)

Независимое множество в теории графов может быть как независимым множеством вершин, так и независимым множеством рёбер. Независимые множества рассматриваются в задачах покрытия графов.

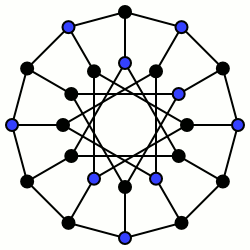
Независимое множество из 9 голубых вершин

Независимое множество вершин

В неориентированном графе $G=(V,E)$ множество его вершин $S$, где $S\subset V$, называется независимым (или внутренне устойчивым), если любые две вершины в нем несмежны, то есть никакая пара вершин не соединена ребром , или другими словами множество $S$ порождает пустой подграф:

$G(S,E^{\prime })\subset G~~\Rightarrow ~~E^{\prime }=\varnothing$

Наибольшее число вершин в таких множествах называется вершинным числом независимости (иногда просто числом независимости) $\beta _{0}(G)$ графа $G$, то есть, если $Q$ есть семейство всех независимых множеств вершин $S$, то $\beta _{0}(G)=\max\{|S|:S\in Q\}$.

Независимое множество рёбер

В неориентированном графе $G=(V,E)$ множество его рёбер $M$, где $M\subset E$, называется независимым, если никакая пара ребер несмежна или множество $M$ порождает пустой подграф:

$G(V^{\prime },M)\subset G~~\Rightarrow ~~V^{\prime }=\varnothing$

Наибольшее число рёбер в таких множествах называется рёберным числом независимости $\beta _{1}(G)$ графа $G$, то есть, если $W$ есть семейство всех независимых множеств рёбер $M$, то $\beta _{1}(G)=\max\{|M|:M\in W\}$.

Множество независимых рёбер также называют паросочетанием . Поэтому независимое множество $M$, имеющее кардинальное число $\beta _{1}$ называется наибольшим паросочетанием графа $G$.