Минимально критичное остовное дерево (Bnunbgl,uk tjnmncuky kvmkfuky ;yjyfk)

Минимально критичное остовное дерево (англ. minimum bottleneck spanning tree, MBST) во взвешенном неориентированном графе — это остовное дерево, в котором наиболее тяжёлое ребро весит как можно меньше. Критичное ребро^[1] — это самое тяжёлое ребро в остовном дереве. Остовное дерево является минимальным критичным остовным деревом, если граф не содержит остовного дерева с критичным ребром меньшего веса^[2]. Для ориентированного графа аналогичная задача известна как минимально критичное ориентированное остовное дерево (англ. Minimum Bottleneck Spanning Arborescence, MBSA).

Определения

Неориентированные графы

Минимально критичное остовное дерево $G(V,E)$

В неориентированном графе $G(V,E)$ и функция $w:E\to \mathbb {R}$ , пусть S будет множеством всех остовных деревьев $T_{i}$ . Пусть $B(T_{i})$ будет максимальным по весу ребром для любого остовного дерева $T_{i}$ . Мы определяем подмножество минимально критичных остовных деревьев S′ так, что для любого $T_{j}\in S'$ и $T_{k}\in S$ мы имеем $B(T_{j})\leqslant B(T_{k})$ для всех i и k^[3].

Граф на рисунке справа является примером MBST, красные рёбра графа образуют MBST графа $G(V,E)$ .

Ориентированные графы

Ориентированное остовное дерево орграфа $G(V,A)$ — это ориентированное (корневое) дерево, которое содержит ориентированный путь из указанной вершины L в каждую вершину графа. Вершина L называется корнем ориентированного остовного дерева. Критичная дуга — это самая тяжёлая дуга в ориентированном остовном дереве. Ориентированное остовное дерево называется минимально критичным (англ. Minimum Bottleneck Spanning Arborescence, MBSA), если орграф не содержит ориентированного остовного дерева с критичной дугой меньшего веса.

Граф справа является примером MBSA, красные рёбра в графе образуют MBSA графа $G(V,A)$ .

Свойства

Любое минимальное остовное дерево (MST, англ. minimum spanning tree) неизбежно является минимально критичным, но не любое минимально критичное обязательно будет минимальным^[4]^[5].

Алгоритм Камерини для неориентированных графов

Камерини в 1978 году предложил^[6] алгоритм, использующийся для получения минимально критичного остовного дерева (MBST) для данного неориентированного связного взвешенного графа. Алгоритм разбивает все рёбра графа на такие два множества $B$ и $A$ , что веса рёбер из множества $B$ не превосходят весов из множества $A$ . Если подграф $G_{B}$ , состоящий из рёбер множества $B$ , связен, алгоритм рекурсивно ищет MBST в $G_{B}$ , и оно будет являться MBST для исходного графа. Если же $G_{B}$ не связен, алгоритм комбинирует каждую его компоненту связности в новую супервершину, затем рекурсивно вычисляет MBST в графе, образованном этими супервершинами и рёбрами из множества $A$ . Произвольный лес из рёбер множества $B$ , компоненты связности которого совпадают с компонентами связности $G_{B}$ , добавляется в MBST исходного графа. Процесс продолжается, пока в графе не останется единственное ребро, связывающее две (супер-) вершины (оно добавляется в MBST). MBST состоит из всех рёбер, найденных на предыдущих шагах^[5].

Псевдокод

Функция имеет два входных параметра: граф G и массив w весов всех рёбер графа G^[7]. Возвращается множество рёбер, составляющих MBST графа G.

 1  function MBST(граф G, веса w)
 2  E ← множество рёбер графа G 
 3  если | E | = 1 то возвращаем E иначе
 4     A ← половина рёбер из E, чьи веса не меньше, чем медиана веса
 5     B ← E - A
 6     F ← лес графа G_B
 7     если F является остовным деревом то
 8        возвращаем MBST(G_B,w)
 9     иначе
 10       возвращаем  $MBST((G_{A})_{\eta },w)\cup F$

Выше $(G_{A})_{\eta }$ является подграфом, составленным из супервершин (трактуя вершины в несвязной компоненте как одну вершину) и рёбер из A.

Время работы

Алгоритм работает за время O(E), где E является числом рёбер. Эта граница достигается за счёт того, что

рёбра разбиваются на два множества с помощью алгоритма поиска медианы за время O(E)
находится лес за время O(E)
рассматривается половина рёбер множества E на каждой итерации, $O(E+E/2+E/4+\dots +1)=O(E)$

Пример

На следующем примере зелёные рёбра используются для образования MBST, а красные штриховые области показывают супервершины, полученные при работе алгоритма.

	Алгоритм делит пополам множество рёбер с учётом весов. Зелёным цветом показаны рёбра, вес которых мал насколько это возможно.
	Имеется остовное дерево в подграфе, образованном исключительно рёбрами из меньшего набора рёбер. Повторяем поиск MBST в этом подграфе.
	Нет остовного дерева в текущем подграфе, образованном рёбрами в текущем меньшем наборе рёбер. Комбинируем вершины разъединённых компонент с супервершинами (показаны красным пунктиром), а затем находим MBST в подграфе, образованном супервершинами и рёбрами в большем наборе рёбер. Лес, образованный каждой разъединённой компонентой, будет частью MBST исходного графа.
	Повторяем аналогичные шаги путём комбинирования вершин в супервершины.
	Алгоритм получает MBST из рёбер, найденных по ходу работы алгоритма.

Алгоритмы MBSA для ориентированных графов

Есть два алгоритма для ориентированных графов — алгоритм Камерини для поиска MBSA и алгоритм Габова и Тарьяна^[5].

Алгоритм Камерини для MBSA

Для ориентированного графа алгоритм Камерини фокусируется на нахождении множества рёбер, которые имеют максимальную критичную цену MBSA. Делается это путём разбиения множества рёбер E на два множества A и B и поддержки множества T, которое является множеством, для которого известно, что G_T не имеет ориентированного остовного дерева. Множество T расширяется множеством B, если максимальное ориентированное остовное дерево графа $G(B\cup T)$ не является ориентированным остовным деревом графа G, в противном случае мы уменьшаем множество E, удаляя A. Общая сложность алгоритма по времени выполнения равна $O(E\log E)$ ^[6]^[5].

Псевдокод

 1  function MBSA(G, w, T)
 2  E ← множество рёбер графа G; 
 3  если | E - T | > 1 то
 4     A ← UH(E-T);
 5     B ← (E - T) - A;
 6     F ← BUSH(G_BUT);
 7     если F является ориентированным остовным деревом графа G то
 8        S ← F; MBSA((G_BUT),w,T);
 9     иначе
 10       MBSA(G,w,TUB);

T представляет подмножество E, для которого известно, что $G_{T}$ не содержит какого-либо ориентированного остовного дерева с корнем в вершине «a». Первоначально T пусто
UH берёт множество (E-T) рёбер графа G и возвращает $A\subset (E-T)$ $A\subset (E-T)$ such that:
1. $|A|=\left\lfloor {\frac {(|E-T|)}{2}}\right\rfloor$
2. $W_{a}\geqslant W_{b}$ для a ∈ A и b ∈ B
BUSH(G) возвращает максимальное ориентированное дерево графа G с корнем в вершине «a»
Окончательным результатом будет S

Пример

После первой итерации этого алгоритма мы получаем F и F не является ориентированным остовным деревом графа G, так что выполняем код

MBSA(G,w,T\cup B)

На второй итерации мы получаем

F'

и

F'

снова не является ориентированным остовным деревом графа G, так что выполняем код

MBSA(G,w,T'\cup B')

На третьей итерации мы получаем

F''

и

F''

является ориентированным остовным деревом графа G, так что выполняем код

MBSA(G_{T''\cup B''},w,T'')

MBSA(G_{T''\cup B''},w,T'')

когда мы выполняем

MBSA(G_{T''\cup B''},w,T'')

,

|E-T|

равно 1, а значит не превосходит 1, так что алгоритм возвращает конечный результат, равный

S=F''

.

Алгоритм Габова и Тарьяна для MBSA

Габов и Тарьян предложили образующую MBSA модификацию алгоритма Дейкстры кратчайшего пути с одним источником. Их алгоритм работает за время $O(E+V\log V)$ , если используется фибоначчиева куча^[8].

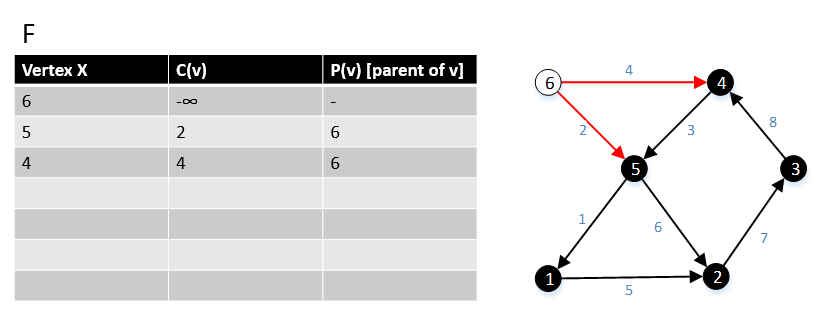
Псевдокод

 Для графа G(V,E), F является набором вершин из V. 
 Начально F = s, где s является стартовой точкой графа G и c(s) = ∞

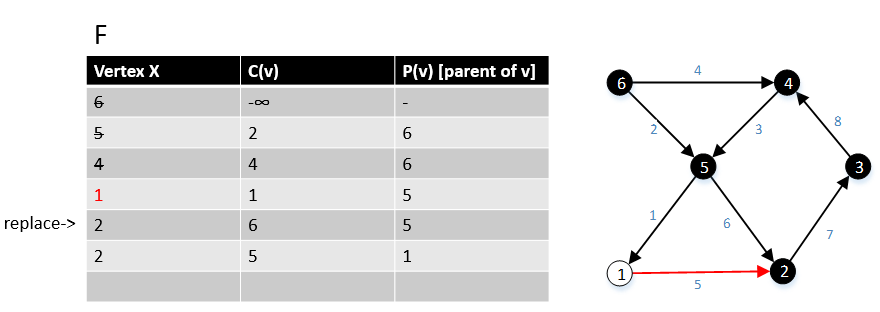
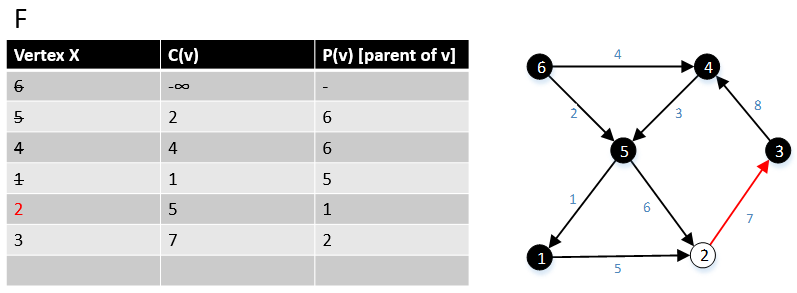
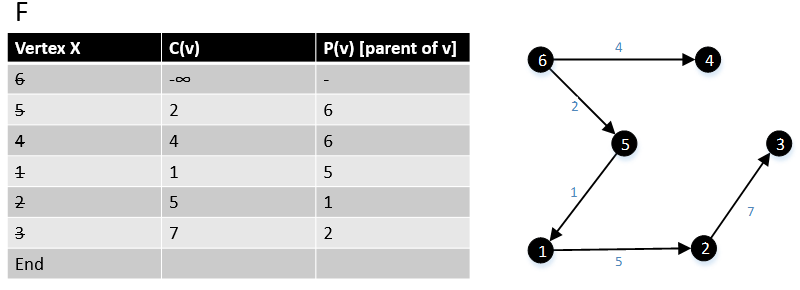
 1  function MBSA-GT(G, w, T)
 2    Выбираем v с минимальным c(v) из F; 
 3    Удаляем его из F;
 4    для всех ребер(v,w) выполняем
 5      если w ∉ F или ∉ Tree то
 6        добавляем w в F;          
 7        c(w) = c(v,w);
 8        p(w) = v;     
 9      иначе
 10       если w ∈ F и c(w) > c(v,w) то
 11         c(w) = c(v,w);
 12         p(w) = v;

Пример

Следующий пример показывает работу алгоритма.

На первом шаге алгоритма мы выбираем корень s из графа G, на рисунке выше вершина 6 является корнем s. Затем мы находим все рёбра (6,w) ∈ E и их цены c(6,w), где w ∈ V.

Переходим в вершину 5 графа G, и находим все рёбра (5,w) ∈ E и их цены cost c(5,w), где w ∈ V.

Переходим в вершину 4 графа G, находим все рёбра (4,w) ∈ E и их цены c(4,w), where w ∈ V. Мы обнаруживаем, что ребро (4,5) > ребра (6,5), так что мы сохраняем ребро (6,5) и удаляем ребро (4,5).

Переходим в вершину 1 графа G, находим все рёбра (1,w) ∈ E и их цены c(1,w), где w ∈ V. Мы обнаруживаем, что ребро (5,2) > ребра (1,2), так что мы удаляем ребро (5,2) и сохраняем ребро (1,2).

Переходим в вершину 2 графа G, находим все рёбра (2,w) ∈ E и их цены c(2,w), где w ∈ V.

Переходим в вершину 3 графа G, находим все рёбра (3,w) ∈ E и их цены c(3,w), где w ∈ V. Мы обнаруживаем, что ребро (3,4) > ребра (6,4), так что мы удаляем ребро (3,4) и сохраняем ребро (6,4).

После просмотра всех вершин графа G алгоритм завершается.

Другой подход предложили Тарьян и Габов с границей $O(E\log ^{*}V)$ для разреженных графов, который очень похож на алгоритм Камерини для MBSA, но вместо разбиения множества рёбер на два множества на каждой итерации, вводятся $K(i)$ , в которых i является числом осуществлённых разбиений, или, другими словами, номер итерации, а $K(i)$ является возрастающей функцией, которая отражает число множеств, которые получаем в результате разбиений на каждой итерации. $K(i)=2^{k(i-1)}$ с $k(1)=2$ . Алгоритм находит $\lambda ^{*}$ , которое является значением веса критичного ребра в любом MBSA. После того, как найдено $\lambda ^{*}$ , любое ориентированное остовное дерево в $G(\lambda ^{*})$ является MBSA, в котором $G(\lambda ^{*})$ является графом, в котором все цены рёбер $\leqslant \lambda ^{*}$ ^[5]^[8].

Примечания

↑ В оригинале — бутылочное горлышко (bottleneck). Иногда переводится как «Минимально узкое остовное дерево», что выглядит не вполне логично.
↑ Everything about Bottleneck Spanning Tree (неопр.). Дата обращения: 9 сентября 2019. Архивировано 5 мая 2018 года.
↑ Murali, 2009.
↑ in question 3 you have a proof for this claim (англ.) (pdf).
↑ ¹ ² ³ ⁴ ⁵ Traboulsi, 2014.
↑ ¹ ² Camerini, 1978, с. 10.
↑ Cui Yuxiang. Minimum Bottleneck Spanning Tree (неопр.) (2013). Дата обращения: 26 сентября 2019. Архивировано 4 марта 2016 года.
↑ ¹ ² Gabow, Tarjan, 1988, с. 411–417.

Литература

Ahmad Traboulsi. Bottleneck Spanning Trees. — 2014. Архивировано 4 марта 2016 года.
Murali T. M. Applications of Minimum Spanning Trees. — 2009.
Camerini P.M. The min-max spanning tree problem and some extensions // Information Processing Letters. — 1978. — Т. 7, вып. 1. — doi:10.1016/0020-0190(78)90030-3.
Harold N. Gabow, Robert E. Tarjan. Algorithms for two bottleneck optimization problems // Journal of Algorithms. — 1988. — Т. 9, вып. 3. — ISSN 0196-6774. — doi:10.1016/0196-6774(88)90031-4.

[1] В оригинале — бутылочное горлышко (bottleneck). Иногда переводится как «Минимально узкое остовное дерево», что выглядит не вполне логично.

[BST-2] Everything about Bottleneck Spanning Tree (неопр.). Дата обращения: 9 сентября 2019. Архивировано 5 мая 2018 года.

[_c0d4e1245d18f7ee-3] Murali, 2009.

[Q3-4] question 3 you have a proof for this claim (англ.) (pdf).

[_af9d892d067b7c65-5] ¹ ² ³ ⁴ ⁵ Traboulsi, 2014.

[_e2af4aa43b5031ff-6] ¹ ² Camerini, 1978, с. 10.

[Cui-7] Cui Yuxiang. Minimum Bottleneck Spanning Tree (неопр.) (2013). Дата обращения: 26 сентября 2019. Архивировано 4 марта 2016 года.

[_824b6660baf8a91e-8] ¹ ² Gabow, Tarjan, 1988, с. 411–417.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]