Кольца Борромео (Tkl,eg >kjjkbyk)

Кольца Борромео
Обозначения
Конвея	[.1]
Александера–Бриггса	632
Многочлены
Джонса	$-q^{3}-q^{-3}+3q^{2}+3q^{-2}-2q-2q^{-1}+4$
Инварианты
Длина косы	6
Число нитей	3
Число пересечений	6
Гиперболический объём	7.327724753
Число отрезков	9
Число развязывания	2
Свойства
Зацепление альтернированное, гиперболическое
Медиафайлы на Викискладе

Кольца Борромео — зацепление, состоящее из трёх топологических окружностей, которые сцеплены и образуют брунново зацепление (то есть удаление любого кольца приведёт к разъединению двух оставшихся колец). Другими словами, никакие два из трёх колец не сцеплены, как в зацеплении Хопфа, тем не менее, все вместе они сцеплены.

Математические свойства

Несмотря на кажущуюся из иллюстраций естественность колец Борромео, из геометрически идеальных окружностей такое зацепление сделать невозможно. Также это можно увидеть, рассмотрев диаграмму узла: если предположить, что окружности 1 и 2 касаются в двух точках пересечения, то они лежат либо в одной плоскости, либо на сфере. В обоих случаях третья окружность должна пересекать эту плоскость или сферу в четырёх точках и не лежать на ней, что невозможно.

Реализация колец Борромео в виде эллипсов

Трёхмерное представление колец Борромео

В то же время подобное зацепление можно осуществить с помощью эллипсов, причём Эксцентриситет этих эллипсов можно сделать сколь угодно малым. По этой причине тонкие кольца, сделанные из гибкой проволоки, можно использовать как кольца Борромео.

Зацепление

Подробнее см. Группа зацепления

В теории узлов кольца Борромео являются простейшим примером бруннова зацепления — хотя любая пара колец не сцеплена, их нельзя расцепить.

Простейший способ это доказать — рассмотреть фундаментальную группу дополнения двух несцеплённых окружностей; по теореме Зейферта — ван Кампена это свободная группа с двумя образующими, a и b, а тогда третьему циклу соответствует класс коммутатора, [a, b] = aba⁻¹b⁻¹, что можно видеть из диаграммы зацепления. Этот коммутатор нетривиален в фундаментальной группе, а потому кольца Борромео сцеплены.

В арифметической топологии существует аналогия между узлами и простыми числами, позволяющая прослеживать связи простых чисел. Тройка простых чисел (13, 61, 937) является связанной по модулю 2 (её символ Редеи равен −1), но попарно по модулю 2 эти числа не связаны (все символы Лежандра равны 1). Такие простые называются «правильными тройками Борромео по модулю 2» или «простыми Борромео по модулю 2».

Гиперболическая геометрия

Кольца Борромео являются примером гиперболического сцепления — дополнение колец Борромео в 3-сфере допускает полную гиперболическую метрику с конечным объёмом. Каноническое разложение (Эпштейна — Пеннера) дополнения состоит из двух правильных октаэдров. Гиперболический объём равен 16Л(π/4) = 7.32772…, где Л — функция Лобачевского.

Связь с косами

Стандартная коса из трёх лент соответствует кольцам Борромео.

Если рассечь кольца Борромео, получим одну итерацию обычного плетения косы. Обратно, если связать концы (одной итерации) обычной косы, получим кольца Борромео. Удаление одного кольца освобождает оставшихся два, и удаление одной ленты из косы освобождает две другие — они являются простейшими брунновым зацеплением и брунновой косой соответственно.

В стандартной диаграмме зацепления кольца Борромео упорядочены в циклическом порядке. Если использовать цвета, как выше, красное будет лежать над зелёным, зелёное над синим, синее над красным, и при удалении одного из колец одно из оставшихся будет лежать над другим и они окажутся незацеплёнными. Так же и с косой: каждая лента лежит над второй и под третьей.

История

Валкнут на Стура-Хаммарском камне

Кольца Борромео как символ христианской Троицы в французской рукописи XIII века

Узел обезьяний кулак

«Мандала» дискордианства, содержащая пять колец Борромео

Дизайн флага Земли Оскара Пернефельда (2015)

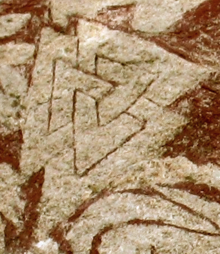
Название «кольца Борромео» появилось из-за их использования на гербе аристократической семьи Борромео в северной Италии. Зацепление много старше и появлялось в виде валкнута на картинных камнях викингов, которые датируются седьмым веком.

Кольца Борромео использовались в различных контекстах, таких как религия и искусство, для того чтобы показать силу единства. В частности кольца использовались как символ Троицы. Известно, что психоаналитик Жак Лакан нашёл вдохновение в кольцах Борромео как модели топологии человеческой личности, в которой каждое кольцо представляет фундаментальный компонент реальности («действительное», «воображаемое» и «символическое»).

В 2006 году Международный математический союз принял решение использовать логотип, основанный на кольцах Борромео, для XXV международного конгресса математиков в Мадриде, Испания.

Каменный столб в храме Марундиисварар в Ченнаи, Тамилнад, Индия, датируемый шестым веком, содержит такую фигуру.

Частичные кольца

Известно много визуальных знаков, относящихся к средним векам и временам ренессанса, состоящих из трёх элементов, сцеплённых друг с другом тем же способом, что и кольца Борромео (в их общепринятом двумерном представлении), но индивидуальные элементы при этом не представляют замкнутых колец. Примерами таких символов служат рога на камне Snoldelev и полумесяцы Дианы де Пуатье. Примером знака с тремя различными элементами служит эмблема клуба Интернасьонал. Хоть и в меньшей степени, к этим символам относятся ганкиил и диаграмма Венна из трёх элементов.

Также узел «обезьяний кулак», по существу, является трёхмерным представлением колец Борромео, хотя узел состоит из трёх уровней.

Большее количество колец

Некоторые соединения в теории узлов содержат множественные конфигурации колец Борромео. Одно соединение такого типа, состоящее из пяти колец, используется в качестве символа в дискордианизме, основанное на изображении из книги «Принципия Дискордия».

Реализации

Структура молекулярных колец Борромео, приведённая в журнале «Science» (2004)

Молекулярные кольца Борромео — молекулярные аналоги колец Борромео, которые являются механически сцеплёнными молекулярными структурами. В 1997 году биолог Мао Чэндэ (Chengde Mao) с соавторами из Нью-Йоркского университета успешно сконструировали кольца из ДНК. В 2003 году химик Фрейзер Стоддарт с соавторами из Калифорнийского университета, использовали комплексные соединения для построения набора колец из 18 компонентов за одну операцию.

Квантово-механический аналог колец Борромео называется ореолом или состоянием Ефимова (существование таких состояний было предсказано физиком Виталием Николаевичем Ефимовым в 1970 году). В 2006 году исследовательская группа Рудольфа Грима и Ганса-Кристофа Нэгерля из Института экспериментальной физики Инсбрукского университета (Австрия) экспериментально подтвердила существование таких состояний в ультрахолодном газе атомов цезия и опубликовала открытие в научном журнале Nature. Группа физиков под руководством Рандалла Хулета (Randall Hulet) в университете Райса в Хьюстоне получили тот же самый результат с помощью трёх связанных атомов лития и опубликовали своё открытие в журнале Science Express. В 2010 году группа под управлением К. Танака получила состояние Ефимова с нейтронами (нейтронный ореол).

См. также

• Контур Похгаммера
• Щит Троицы
• Трикветр

Литература

• Clara Moskowitz. Strange Physical Theory Proved After Nearly 40 Years // Live Science. — 2009. — Вып. December 16.
• K. Tanaka. Observation of a Large Reaction Cross Section in the Drip-Line Nucleus ²²C // Physical Review Letters. — 2010. — Т. 104, вып. 6. — doi:10.1103/PhysRevLett.104.062701.
• T. Kraemer, M. Mark, P. Waldburger, J. G. Danzl, C. Chin, B. Engeser, A. D. Lange, K. Pilch, A. Jaakkola, H.-C. Nägerl and R. Grimm. Evidence for Efimov quantum states in an ultracold gas of caesium atoms // Nature. — 2006. — Т. 440, вып. 7082. — doi:10.1038/nature04626. — . — arXiv:cond-mat/0512394. — PMID 16541068.
• C. Mao, W. Sun, N. C. Seeman. Assembly of Borromean rings from DNA // Nature. — 1997. — Т. 386. — doi:10.1038/386137b0. — PMID 9062186.
• Arul Lakshminarayan. Borromean Triangles and Prime Knots in an Ancient Temple. — Indian Academy of Sciences, 2007. — Вып. May.
• P. R. Cromwell, E. Beltrami and M. Rampichini, «The Borromean Rings», Mathematical Intelligencer Vol. 20 no. 1 (1998) 53-62.
• Michael H. Freedman, Richard Skora. Strange Actions of Groups on Spheres // Journal of Differential Geometry. — 1987. — Т. 25. — С. 75–98.
• Bernt Lindström, Hans-Olov Zetterström. Borromean Circles are Impossible // American Mathematical Monthly. — 1991. — Т. 98, вып. 4. — С. 340–341. — doi:10.2307/2323803. — . Статья объясняет, почему кольца Борромео не могут быть абсолютно круглыми
• R. Brown, J. Robinson. Borromean circles. Letter // American Mathematical Monthly. — 1992. — Вып. 4 (April). — С. 376–377.. Статья показывает, что существуют квадраты Борромео, и эти квадраты были воплощены в скульптуре Джоном Робинсоном, который воплотил и другие формы этой структуры.
• W. W. Chernoff. (English summary) 15th British Combinatorial Conference (Stirling, 1995). // Discrete Math.. — 1997. — Т. 167/168. — С. 197–204. Статья рассматривает другие многоугольники.

Ссылки

• «Borromean Rings Homepage», Dr Peter Cromwell’s website.
• Jablan, Slavik. «Are Borromean Links So Rare?», Visual Mathematics.
• «Borromean Rings», The Knot Atlas.
• «Borromean Rings», The Encyclopedia of Science.
• «Symbolic Sculpture and the Borromean Rings», Sculpture Maths.
  • «African Borromean ring carving», Sculpture Maths.
• «The Borromean Rings: A new logo for the IMU» [w/video], International Mathematical Union
• Hunton, John Higher Linkages and Borromean Rings  (неопр.). Numberphile. Brady Haran. Дата обращения: 20 мая 2015. Архивировано из оригинала 24 мая 2013 года.
• Кольца Борромео на сайте «Невозможный мир»