Задачи теории решёток ({g;gcn mykjnn jyo~mkt)

Задачи теории решёток — это класс задач оптимизации на решётках (то есть дискретных аддитивных подгруппах, заданных на множестве $\mathbb {R} ^{n}$ ). Гипотетическая плохая разрешимость таких задач является центральным местом для построения стойких криптосистем на решётках. Для приложений в таких криптосистемах обычно рассматриваются решётки на векторных пространствах (часто $\mathbb {Q} ^{n}$ ) или свободных модулях (часто $\mathbb {Z} ^{n}$ ).

Для всех задач ниже допустим, что нам даны (кроме других более конкретных входных данных) базис для векторного пространства V и норма N. Для норм обычно рассматривается L². Однако другие нормы, такие как L^p), также рассматриваются и появляются в различных результатах^[1]. Ниже в статье $\lambda (L)$ означает длину самого короткого вектора в решётке L, то есть

\lambda (L)=\min _{v\in L\setminus \{\mathbf {0} \}}\|v\|_{N}.

Задача нахождения кратчайшего вектора (ЗКВ)

Иллюстрация задачи нахождения кратчайшего вектора (базисные векторы показаны синим цветом, кратчайший вектор показан красным).

В ЗКВ (англ. Shortest vector problem, SVP), для решётки L даны базис векторного пространства V и норма N (часто L²) и нужно найти ненулевой вектор минимальной длины в V по норме N в решётке L. Другими словами, выходом алгоритма должен быть ненулевой вектор v, такой, что $N(v)=\lambda (L)$ .

В $\gamma$ -приближённой версии ЗКВ_γ нужно найти ненулевой вектор решётки длины, не превосходящий $\gamma \lambda (L)$ .

Трудность

Только точная версия задачи, как известно, является NP-трудной для рандомизированного сведе́ния^[2]^[2].

Для контраста, известно, что эквивалентная задача для равномерных норм, является NP-трудной^[3].

Алгоритмы для евклидовых норм

Для решения точной версии ЗКВ для евклидовой нормы известны несколько различных подходов, которые можно разбить на два класса — алгоритмы, требующие суперэкспоненциального времени ( $2^{\omega (n)}$ ) и $\operatorname {poly} (n)$ памяти, и алгоритмы, требующие экспоненциального времени и памяти ( $2^{\Theta (n)}$ ), от размерности решётки. В первом классе алгоритмов наиболее значимы алгоритмы перечисления решётки^[4]^[5]^[6] и алгоритмы сокращения случайных выборок^[7]^[8], в то время как второй класс включает решеточное просеивание^[9]^[10]^[11], вычисление ячеек Вороного на решётке^[12]^[13] и дискретные гауссовы распределения^[14]. Открытой проблемой является, существуют ли алгоритмы, решающие точную ЗКВ за обычное экспоненциальное время ( $2^{O(n)}$ ) и требующие память, полиномиально зависящую от размерности решётки^[15].

Для решения $\gamma$ -приближённой версии ЗКВ_γ для $\gamma >1$ для евклидовой нормы лучший известный подход базируется на использовании редукции базиса решётки^[англ.]. Для больших $\gamma =2^{\Omega (n)}$ Алгоритм Ленстры — Ленстры — Ловаса редукции базиса решётки может найти решение за полиномиальное время от размерности решётки. Для малых значений $\gamma$ обычно используется блочный алгоритм Коркина — Золотарёва (БКЗ, англ. Block Korkine-Zolotarev algorithm, BKZ)^[16]^[17]^[18], где вход алгоритма (размер блока $\beta$ ) определяет временну́ю сложность и качество выхода — для больших аппроксимационных коэффициентов $\gamma$ достаточен малый размер блока $\beta$ и алгоритм завершается быстро. Для малых $\gamma$ требуется больший $\beta$ , чтобы найти достаточно короткие вектора решётки, и алгоритм работает дольше. БКЗ-алгоритм внутри использует алгоритм точного ЗКВ в качестве подпрограммы (работающей на решётке размерности, не превосходящей $\beta$ ), и общая сложность тесно связана со стоимостью этих вызовов ЗКВ в размерности $\beta$ .

GapSVP

Задача $GapSVP_{\beta }$ состоит в различении между вариантами ЗКВ, в которых ответ не превосходит 1 или больше $\beta$ , где $\beta$ может быть фиксированной функцией от размерности решётки $n$ . Если задан базис решётки, алгоритм должен решить, будет $\lambda (L)\leqslant 1$ или $\lambda (L)>\beta$ . Подобно другим задачам с предусловиями^[англ.], алгоритму разрешены ошибки во всех остальных случаях.

Другой версией задачи является $GapSVP_{\zeta ,\gamma }$ для некоторых функций $\zeta ,\gamma$ . Входом алгоритма является базис $B$ и число $d$ . Алгоритм обеспечивает, чтобы все вектора в ортогонализации Грама — Шмидта имели длину, не меньшую 1, чтобы $\lambda (L(B))\leqslant \zeta (n)$ и чтобы $1\leqslant d\leqslant \zeta (n)/\gamma (n)$ , где $n$ — размерность. Алгоритм должен принять, если $\lambda (L(B))\leqslant d$ и отвергнуть, если $\lambda (L(B))\geqslant \gamma (n).d$ . Для больших $\zeta$ ( $\zeta (n)>2^{n/2}$ ) задача эквивалентна $GapSVP_{\gamma }$ , поскольку^[19] препроцессорный шаг с помощью алгоритма ЛЛЛ делает второе условие (а следовательно, $\zeta$ ) лишним.

Задача нахождения ближайшего вектора (ЗБВ)

Иллюстрация задачи нахождения ближайшего вектора (базисные вектора показаны синим цветом, ближайший вектор показан красным, внешний вектор показан зелёным).

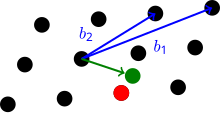
В ЗБВ (англ. Closest vector problem, CVP) для решётки L даны бaзис векторного пространства V и метрика M (часто L²), а также вектор v в V, но не обязательно в L. Требуется найти вектор в L, наиболее близкий к v (по мере M). В $\gamma$ -приближённой версии ЗБВ_γ, нужно найти вектор решётки на расстоянии, не превосходящем $\gamma$ .

Связь с ЗКВ

Задача нахождения ближайшего вектора является обобщением задачи нахождения кратчайшего вектора. Легко показать, что если задан предсказатель для ЗБВ_γ (определён ниже), можно решить ЗКВ_γ путём некоторых запросов предсказателю^[20]. Естественный метод поиска кратчайшего вектора путём запросов к предсказателю ЗБВ_γ, чтобы найти ближайший вектор, не работает, поскольку 0 является вектором решётки и алгоритм, потенциально, может вернуть 0.

Сведение от ЗКВ_γ к ЗБВ_γ следующее: Предположим, что входом задачи ЗКВ_γ является базис решётки $B=[b_{1},b_{2},\ldots ,b_{n}]$ . Рассмотрим базис $B^{i}=[b_{1},\ldots ,2b_{i},\ldots ,b_{n}]$ и пусть $x_{i}$ будет вектором, который вернул алгоритм ЗБВ $\gamma (B^{i},b_{i})$ . Утверждается, что кратчайший вектор в множестве $\{x_{i}-b_{i}\}$ является кратчайшим вектором в данной решётке.

Трудность

Голдрайх, Миссиансио, Сафра и Seifert показали, что из любой сложности ЗКВ вытекает такая же сложность для ЗБВ^[21]. Используя средства ВПД^[англ.], Арора , Babai, Stern, Sweedyk показали, что ЗБВ трудна для аппроксимации до множителя $2^{\log ^{1-\epsilon }(n)}$ , если только не $\operatorname {NP} \subseteq \operatorname {DTIME} (2^{poly(\log n)})$ ^[22]. Динур, Киндлер, Сафра усилили это, указав NP-трудность с $\epsilon =(\log \log n)^{c}$ для $c<1/2$ ^[23].

Сферическое декодирование

Алгоритм для ЗБВ, особенно вариант Финке и Поста^[5] используется, например, для обнаружения данных в беспроводных системах связи с многоканальным входом/многоканальным выходом (MIMO) (для кодированных и раскодированных сигналов)^[24]^[12]. В этом контексте он называется сферическим декодированием^[25].

Алгоритм был применён в области целочисленного разрешения неоднозначности фазы несущей GNSS (GPS)^[26]. В этой области это называется LAMBDA-методом.

GapCVP

Эта задача подобна задаче GapSVP. Для $GapCVP_{\beta }$ , входом является базис решётки и вектор $v$ , а алгоритм должен ответить, какое из условий выполняется

существует вектор решётки, такой, что расстояние между ним и $v$ не превосходит 1.
любой вектор решётки находится от $v$ на расстоянии, большем $\beta$ .

Известные результаты

Задача тривиально содержится в классе NP для любого коэффициента аппроксимации.

Клаус Шнорр^[англ.] в 1987 показал, что алгоритмы с детерминированным полиномиальным временем могут решить задачу для $\beta =2^{O(n(\log \log n)^{2}/\log n)}$ ^[27]. Айтаи, Кумар, Сивакумар показали, что вероятностные алгоритмы могут получить слегка более лучший аппроксимационный коэффициент $\beta =2^{O(n\log \log n/\log n)}$ ^[9].

В 1993 Банашчик показал, что $GapCVP_{n}$ содержится в $NP\cap coNP$ ^[28]. В 2000 Голдрайх и Голдвассер показали, что $\beta ={\sqrt {n/\log n}}$ помещает задачу в классы как NP, так и coAM^[29]. В 2005 Ааронов и Реджев показали, что для некоторой константы $c$ задача с $\beta =c{\sqrt {n}}$ входит в $NP\cap coNP$ ^[30].

Для нижних границ Динур, Киндлер и Сафра показали в 1998, что задача является NP-трудной для $\beta =n^{o(1/\log {\log {n}})}$ ^[31].

Задача о кратчайших независимых векторах

Если дана решётка L размерности n, алгоритм должен выдать n линейно независимых векторов $v_{1},v_{2},\ldots ,v_{n}$ , таких, что $\max \|v_{i}\|<\max _{B}\|b_{i}\|$ , где правая часть состоит из всех базисов $B=\{b_{1},\ldots ,b_{n}\}$ решётки.

В $\gamma$ -приближённой версии, если дана решётка L размерности n, алгоритм находит n линейно независимых векторов $v_{1},v_{2},\ldots ,v_{n}$ длины $\max ||v_{i}||\leqslant \gamma \lambda _{n}(L)$ , где $\lambda _{n}(L)$ является $n$ -ым последующим минимумом $L$ .

Декодирование с ограниченным расстоянием

Эта задача подобна ЗБВ. Если дан вектор, такой, что его расстояние от решётки не превосходит $\lambda (L)/2$ , алгоритм должен выдать ближайший вектор решётки.

Задача покрытия решётки радиусами

Если дан базис для решётки, алгоритм должен найти самое большое расстояние (или, в некоторых версиях, его аппроксимацию) от любого вектора до решётки.

Задача поиска кратчайшего базиса

Многие задачи становятся проще, если входной базис состоит из коротких векторов. Алгоритм, который решает задачу поиска кратчайшего базиса (ПКБ), должен по заданному базису решётки $B$ дать эквивалентный базис $B'$ , такой, что длина самого длинного вектора в $B'$ настолько коротка, насколько возможно.

Аппроксимированная версия задачи ПКБ_γ заключается в поиске базиса, самый длинный вектор которого не превосходит по длине в $\gamma$ раз самого длинного вектора в кратчайшем базисе.

Использование в криптографии

Трудность среднего случая^[англ.] задач образует базис для доказательства стойкости большинства криптографических схем. Однако экспериментальные данные наталкивают на предположение, что для большинства NP-трудных задач это свойство отсутствует — они трудны лишь в худшем случае. Для многих задач теории решёток было предположено или доказано, что они трудны в среднем, что делает их привлекательными для криптографических схем. Однако трудность в худшем случае некоторых задач теории решёток используется для создания схем стойкой криптографии. Использование трудности в худшем случае в таких схемах помещает их в класс очень немногих схем, которые, с большой долей вероятности, устойчивы даже для квантовых компьютеров.

Вышеприведённые задачи теории решёток легко решаются, если дан «хороший» базис. Цель алгоритмов редукции базиса^[англ.] по данному базису решётки выдать новый базис, состоящий из относительно коротких почти ортогональных векторов. Алгоритм Ленстры — Ленстры — Ловаса редукции базиса решётки (ЛЛЛ, англ. Lenstra–Lenstra–Lovász lattice basis reduction algorithm, LLL) был ранним эффективным алгоритмом для этой задачи, который может выдать редуцированный базис решётки за полиномиальное время^[32]. Этот алгоритм и его дальнейшие улучшения были использованы для взлома некоторых криптографических схем, что сформировало его статус как очень важного средства в криптографии. Успех ЛЛЛ на экспериментальных данных привел к вере, что редукция базиса решётки на практике может быть простой задачей. Однако эта вера была разрушена, когда в конце 1990s-х были получены новые результаты о трудности задач теории решёток, начиная с результатов Айтаи^[33].

В своей основополагающей работе Айтаи показал, что ЗКВ был NP-трудным и обнаружил некоторые связи между сложностью в худшем случае и сложностью в среднем некоторых задач теории решёток^[2]. Основываясь на этих результатах, Айтаи и Дворк создали криптосистему с открытым ключом, секретность которой может быть доказана, используя лишь худший случай трудности определённой версии ЗКВ^[34], что было первым результатом по созданию защищённых систем с использованием трудности в худшем случае^[35].

См. также

Обучение с ошибками

Примечания

↑ Khot, 2005, с. 789–808.
↑ ¹ ² ³ Ajtai, 1998, с. 10–19.
↑ van Emde Boas, 1981.
↑ Kannan, 1983, с. 193–206.
↑ ¹ ² Fincke, Pohst, 1985, с. 463–471.
↑ Gama, Nguyen, Regev, 2010, с. 257–278.
↑ Schnorr, 2003, с. 145–156.
↑ Aono, Nguyen, 2017, с. 65–102.
↑ ¹ ² Ajtai, Kumar, Sivakumar, 2001, с. 601–610.
↑ Micciancio, Voulgaris, 2010, с. 1468–1480.
↑ Becker, Ducas, Gama, Laarhoven, 2015, с. 10–24.
↑ ¹ ² Agrell, Eriksson, Vardy, Zeger, 2002, с. 2201–2214.
↑ Micciancio, Voulgaris, 2010a, с. 351–358.
↑ Aggarwal, Dadush, Regev, Stephens-Davidowitz, 2015, с. 733–742.
↑ Micciancio, 2017.
↑ Schnorr, 1987, с. 201–224.
↑ Schnorr, Euchner, 1994, с. 181–199.
↑ Chen, Nguyen, 2011, с. 1–20.
↑ Peikert, 2009, с. 333–342.
↑ Micciancio, Goldwasser, 2002.
↑ Goldreich, Micciancio, Safra, Seifert, 1999, с. 55–61.
↑ Arora, Babai, Stern, Sweedyk, 1997, с. 317–331.
↑ Dinur, Kindler, Safra, 2003, с. 205–243.
↑ Biglieri, Calderbank, Constantinides, Goldsmith, Paulraj, Poor, 2007.
↑ Wang, Le-Ngoc, 2011, с. 189–200.
↑ Hassibi, Boyd, 1998, с. 2938–2952.
↑ Schnorr, 1993.
↑ Banaszczyk, 1993, с. 625–635.
↑ Goldreich, Goldwasser, 1998, с. 1–9.
↑ Aharonov, Regev, 2005.
↑ Dinur, Kindler, Safra, 1998, с. 99.
↑ Lenstra, Lenstra, Lovász, 1982, с. 515–534.
↑ Ajtai, 1996, с. 99–108.
↑ Ajtai, Dwork, 1997, с. 284–293.
↑ Cai, 2000, с. 1–32.

Литература

Subhash Khot. Hardness of approximating the shortest vector problem in lattices // J. ACM. — 2005. — Т. 52, вып. 5. — doi:10.1145/1089023.1089027.
Miklós Ajtai. The shortest vector problem in L₂ is NP-hard for randomized reductions // Proceedings of the thirtieth annual ACM symposium on Theory of computing. — Dallas, Texas, United States: ACM, 1998.
Peter van Emde Boas. Another NP-complete problem and the complexity of computing short vectors in a lattice. Technical Report 8104. — University of Amsterdam, Department of Mathematics, Netherlands, 1981.
Chris Peikert. Public-key cryptosystems from the worst-case shortest vector problem: extended abstract // Proceedings of the 41st annual ACM symposium on Theory of Computing. — Bethesda, MD, USA: ACM, 2009.
Daniele Micciancio, Shafi Goldwasser. Complexity of Lattice Problems: A Cryptographic Perspective. — 2002. — Т. 671. — (Kluwer International Series in Engineering and Computer Science). — ISBN 0792376889.
- Daniele Micciancio, Shafi Goldwasser. Complexity of Lattice Problems: A Cryptographic Perspective. — Springer US, 2011. — (The Springer International Series in Engineering and Computer Science). — ISBN 9781461508984.
Goldreich O., Micciancio D., Safra S., Seifert J. -p. Approximating shortest lattice vectors is not harder than approximating closest lattice vectors // Inf. Process. Lett.. — 1999. — Т. 71, вып. 2. — doi:10.1016/S0020-0190(99)00083-6.
Oded Goldreich, Shafi Goldwasser. On the limits of non-approximability of lattice problems // Proceedings of the thirtieth annual ACM symposium on Theory of computing. — Dallas, Texas, United States: ACM, 1998.

Sanjeev Arora, László Babai, Jacques Stern, Z. Sweedyk. The hardness of approximate optima in lattices, codes, and systems of linear equations // J. Comput. Syst. Sci.. — 1997. — Т. 54, вып. 2. — doi:10.1109/SFCS.1993.366815.
Dinur I., Kindler G., Safra S. Approximating CVP to Within Almost-Polynomial Factors is NP-Hard // Combinatorica. — 2003. — Т. 23, вып. 2. — doi:10.1007/s00493-003-0019-y.
Dinur I., Kindler G., Safra S. Approximating-CVP to within Almost-Polynomial Factors is NP-Hard // Proceedings of the 39th Annual Symposium on Foundations of Computer Science. — IEEE Computer Society, 1998. — ISBN 0-8186-9172-7.

Fincke U., Pohst M. Improved Methods for Calculating Vectors of Short Length in a Lattice, Including a Complexity Analysis // Math. Comp.. — 1985. — Т. 44, вып. 170. — doi:10.1090/S0025-5718-1985-0777278-8.
Biglieri E., Calderbank R., Constantinides A., Goldsmith A., Paulraj A., Poor H. V. MIMO Wireless Communications. — Cambridge: Cambridge U. P., 2007.
Ping Wang, Tho Le-Ngoc. A List Sphere Decoding Algorithm with Improved Radius Setting Strategies // Wireless Personal Communications. — 2011. — Т. 61, вып. 1. — doi:10.1007/s11277-010-0018-4.
Hassibi A., Boyd S. Integer Parameter Estimation in Linear Models with Applications to GPS // IEEE Trans. Sig. Proc.. — 1998. — Т. 46, вып. 11. — doi:10.1109/78.726808.
Miklós Ajtai, Ravi Kumar, D. Sivakumar. A sieve algorithm for the shortest lattice vector problem // Proceedings of the thirty-third annual ACM symposium on Theory of computing. — Hersonissos, Greece: ACM, 2001.
Banaszczyk W. New bounds in some transference theorems in the geometry of numbers // Math. Ann.. — 1993. — Т. 296, вып. 1. — doi:10.1007/BF01445125.
Dorit Aharonov, Oded Regev. Lattice problems in NP $\cap$ coNP // J. ACM. — 2005. — Т. 52, вып. 5. — doi:10.1145/1089023.1089025.
Ajtai M. Generating hard instances of lattice problems // Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. — Philadelphia, Pennsylvania, United States: ACM, 1996.
Miklós Ajtai, Cynthia Dwork. A public-key cryptosystem with worst-case/average-case equivalence // Proceedings of the twenty-ninth annual ACM symposium on Theory of computing. — El Paso, Texas, United States: ACM, 1997.
Jin-Yi Cai. The Complexity of Some Lattice Problems // Algorithmic Number Theory. — 2000. — Т. 1838. — doi:10.1007/10722028_1.
Lenstra A. K., Lenstra H. W., Lovász L. Factoring polynomials with rational coefficients // Math. Ann.. — 1982. — Т. 261, вып. 4. — doi:10.1007/BF01457454.
Ravi Kannan. Improved Algorithms for Integer Programming and Related Lattice Problems // Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing. — New York, NY, USA: ACM, 1983. — (STOC). — ISBN 0897910990. — doi:10.1145/800061.808749.
Nicolas Gama, Phong Q. Nguyen, Oded Regev. Lattice Enumeration Using Extreme Pruning // Advances in Cryptology – EUROCRYPT 2010. — Springer, Berlin, Heidelberg, 2010. — doi:10.1007/978-3-642-13190-5_13.
Yoshinori Aono, Phong Q. Nguyen. Random Sampling Revisited: Lattice Enumeration with Discrete Pruning // Advances in Cryptology – EUROCRYPT 2017. — Springer, Cham, 2017. — doi:10.1007/978-3-319-56614-6_3.
Daniele Micciancio, Panagiotis Voulgaris. Faster Exponential Time Algorithms for the Shortest Vector Problem // Proceedings of the Twenty-first Annual ACM-SIAM Symposium on Discrete Algorithms. — Philadelphia, PA, USA: Society for Industrial and Applied Mathematics, 2010. — С. 1468–1480. — (SODA '10). — ISBN 9780898716986.
Daniele Micciancio, Panagiotis Voulgaris. A Deterministic Single Exponential Time Algorithm for Most Lattice Problems Based on Voronoi Cell Computations // Proceedings of the Forty-second ACM Symposium on Theory of Computing. — New York, NY, USA: ACM, 2010a. — ISBN 9781450300506. — doi:10.1145/1806689.1806739.
Becker A., Ducas L., Gama N., Laarhoven T. Proceedings of the Twenty-Seventh Annual ACM-SIAM Symposium on Discrete Algorithms. — Society for Industrial and Applied Mathematics, 2015. — С. 10–24. — (Proceedings). — doi:10.1137/1.9781611974331.ch2.
Divesh Aggarwal, Daniel Dadush, Oded Regev, Noah Stephens-Davidowitz. Solving the Shortest Vector Problem in 2N Time Using Discrete Gaussian Sampling: Extended Abstract // Proceedings of the Forty-seventh Annual ACM Symposium on Theory of Computing. — New York, NY, USA: ACM, 2015. — (STOC). — ISBN 9781450335362. — doi:10.1145/2746539.2746606.
Daniele Micciancio. Lattice Cryptography – Shortest Vector Problem. — 2017.
Schnorr C. P. A hierarchy of polynomial time lattice basis reduction algorithms // Theoretical Computer Science. — 1987. — Vol. 53. — Вып. 2. — doi:10.1016/0304-3975(87)90064-8.
Schnorr C. P., Euchner M. Lattice basis reduction: Improved practical algorithms and solving subset sum problems // Mathematical Programming. — 1994. — Т. 66, вып. 1-3. — ISSN 0025-5610. — doi:10.1007/bf01581144.
Claus Peter Schnorr. Lattice Reduction by Random Sampling and Birthday Methods // STACS. — Springer, Berlin, Heidelberg, 2003. — ISBN 3540364943. — doi:10.1007/3-540-36494-3_14.
Schnorr C. P. Factoring integers and computing discrete logarithms via diophantine approximation // . — 1993. — Т. 13. — С. 171-181.. — (AMS DIMACS series in Disc. Math, and Theoretical Comp. Science).
Yuanmi Chen, Phong Q. Nguyen. Advances in Cryptology – ASIACRYPT 2011. — Springer, Berlin, Heidelberg, 2011. — doi:10.1007/978-3-642-25385-0_1.

Литература для дальнейшего чтения

Agrell E., Eriksson T., Vardy A., Zeger K. Closest Point Search in Lattices // IEEE Trans. Inform. Theory. — 2002. — Т. 48, вып. 8. — doi:10.1109/TIT.2002.800499.
Daniele Micciancio. The Shortest Vector Problem is {NP}-hard to approximate to within some constant // SIAM Journal on Computing. — 2001. — Т. 30, вып. 6. — С. 2008–2035. — doi:10.1137/S0097539700373039.
Phong Q. Nguyen, Jacques Stern. Lattice Reduction in Cryptology: An Update // Proceedings of the 4th International Symposium on Algorithmic Number Theory. — Springer-Verlag, 2000. — С. 85–112. — ISBN 3-540-67695-3.

[_76d7a3fc95d18beb-1] Khot, 2005, с. 789–808.

[_35fc81b48f9aba11-2] ¹ ² ³ Ajtai, 1998, с. 10–19.

[_5de7efa62106d995-3] van Emde Boas, 1981.

[_88100c12eec92b83-4] Kannan, 1983, с. 193–206.

[_e63e019d457d59b4-5] ¹ ² Fincke, Pohst, 1985, с. 463–471.

[_e5057f35fe426eeb-6] Gama, Nguyen, Regev, 2010, с. 257–278.

[_5e77c06238a7b97e-7] Schnorr, 2003, с. 145–156.

[_606181a5954f08ed-8] Aono, Nguyen, 2017, с. 65–102.

[_428e2332d8bdd079-9] ¹ ² Ajtai, Kumar, Sivakumar, 2001, с. 601–610.

[_279065467f396cea-10] Micciancio, Voulgaris, 2010, с. 1468–1480.

[_fca396d61aaa869d-11] Becker, Ducas, Gama, Laarhoven, 2015, с. 10–24.

[_8ad39e9d008e5bbc-12] ¹ ² Agrell, Eriksson, Vardy, Zeger, 2002, с. 2201–2214.

[_eb2214b49e6ce7cc-13] Micciancio, Voulgaris, 2010a, с. 351–358.

[_7cd8a08fa1b2bc9e-14] Aggarwal, Dadush, Regev, Stephens-Davidowitz, 2015, с. 733–742.

[_41e26bd7f5e5d8e2-15] Micciancio, 2017.

[_82e6954ebc60faed-16] Schnorr, 1987, с. 201–224.

[_46379de0f9e832ef-17] Schnorr, Euchner, 1994, с. 181–199.

[_f929d9a425053c33-18] Chen, Nguyen, 2011, с. 1–20.

[_4bb0c16c7028f78f-19] Peikert, 2009, с. 333–342.

[_0af9de51ba28db7b-20] Micciancio, Goldwasser, 2002.

[_4007ad819000687a-21] Goldreich, Micciancio, Safra, Seifert, 1999, с. 55–61.

[_320b3ed7ea7332c8-22] Arora, Babai, Stern, Sweedyk, 1997, с. 317–331.

[_da478c111e8a60cb-23] Dinur, Kindler, Safra, 2003, с. 205–243.

[_06d0140c78f9e92e-24] Biglieri, Calderbank, Constantinides, Goldsmith, Paulraj, Poor, 2007.

[_ae56ef35139c27da-25] Wang, Le-Ngoc, 2011, с. 189–200.

[_ff19d65505add506-26] Hassibi, Boyd, 1998, с. 2938–2952.

[_a9683db3a3508e94-27] Schnorr, 1993.

[_53c54775a5c46c55-28] Banaszczyk, 1993, с. 625–635.

[_fda89f77042111b7-29] Goldreich, Goldwasser, 1998, с. 1–9.

[_cff72330eb175147-30] Aharonov, Regev, 2005.

[_f66798fb288c1ea8-31] Dinur, Kindler, Safra, 1998, с. 99.

[_e2c836c9995de0db-32] Lenstra, Lenstra, Lovász, 1982, с. 515–534.

[_b0e9d38f6db0fb13-33] Ajtai, 1996, с. 99–108.

[_bb522fdfd8214bb6-34] Ajtai, Dwork, 1997, с. 284–293.

[_24f89b29692eb243-35] Cai, 2000, с. 1–32.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]