Задача об освещении ({g;gcg kQ kvfypyunn)
Перейти к навигации
Перейти к поиску
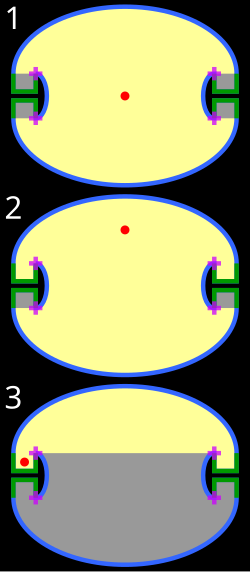
Решение Роджера Пенроуза.
Задача об освещении — вопрос Эрнста Штрауса сформулированный им в 1950-х годах.[1]
- В плоской фигуре (комнате) с зеркальными сторонами есть точечный источник света. Верно ли что любая точка фигуры освещена?
Решения
[править | править код]
- Для случая комнаты с гладкой границей ответ отрицательный;
- Более того можно построить пример комнаты неосвещаемой полностью из любой её точки; пример с двумя дугами эллипсов показан на рисунке. Этот пример был построен Роджером Пенроузом в 1958 году и переоткрыт Виктором Кли в 1979.[2][1][3]
- Пример многоугольной комнаты, построенный Джорджем Токарским в 1995 году, имеет точку куда свет не доходит, при этом считается, что углы комнаты поглощают свет.[4]
-
- Подобный пример построен им же в размерности 3.
- Позже Д. Кастро построил пример с меньшим числом сторон.[5]
- Источником света в многоугольной комнате с рациональными (в градусах) углами будет освещать всю комнату, за возможным исключением конечного числа точек.[6]
Примечания
[править | править код]- ↑ 1 2 Weisstein. Illumination Problem. Wolfram Research. Дата обращения: 19 декабря 2010. Архивировано 4 июня 2011 года.
- ↑ Lionel Penrose and Roger Penrose, Puzzles for christmas, New Scientist 25 (1958), 1580—1581.
- ↑ Klee, Victor Some unsolved problems in plane geometry. Math. Mag. 52 (1979), no. 3, 131–145.
- ↑ George; Tokarsky. Polygonal Rooms Not Illuminable from Every Point (англ.) // American Mathematical Monthly : journal. — Mathematical Association of America, 1995. — December (vol. 102, no. 10). — P. 867—879. — doi:10.2307/2975263.
- ↑ David; Castro. Corrections (неопр.) // Quantum Magazine[англ.]. — Springer-Verlag. — Т. 7, № 3. — С. 42. Архивировано 30 июня 2019 года.
- ↑ Samuel; Lelièvre. Everything is illuminated (англ.) // Geometry & Topology : journal. — 2016. — 4 July (vol. 20, no. 3). — P. 1737—1762. — doi:10.2140/gt.2016.20.1737. — arXiv:1407.2975.

