Задача Келети о квадратах ({g;gcg Tylymn k tfg;jgmg])
Перейти к навигации
Перейти к поиску
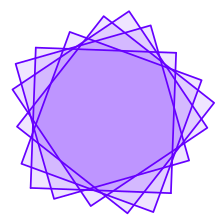
Контрпример из пяти квадратов, построенный Киссом и Виднявским.

Задача Келети — вопрос комбинаторной геометрии про верхнюю оценку на отношение периметра к площади объединения равных квадратов. Сформулирован Тамасом Келети в 1998 году.[1] В 2014 году был найден контрпример.
Формулировка
[править | править код]Предположим — объединение конечного числа единичных квадратов на плоскости. Верно ли, что
где обозначает периметр, а площадь .
Замечания
[править | править код]- Если все у всех квадратов совпадают центры, то выполняется равенство.
История
[править | править код]- Тамас Келети доказал, что отношение ограничено сверху некоторой константой.
- Генеш[2][3] доказал, что
- Он также доказал,
- в трёх случаях:
- если все квадраты из семейства получаются друг из друга параллельным переносом,
- если квадраты имею общий центр
- если число квадратов равно 2.
- В 2014 году, Виктор Кисс и Золтен Виндянски построили контрпример из 5 квадратов. Они также построили пример с отношением около .[4]
Вариации и обобщения
[править | править код]- По теореме Келети, для данного многоугольника K, частное периметра к площади у произвольного объединения многоугольников равных K, ограничено сверху.
- Аналогичные задачи для правильных многоугольников также имеют контрпримеры. То есть для правильного многоугольника K существует конечный набор равных многоугольников с объединением F такой, что
Примечания
[править | править код]- ↑ T. Keleti, A covering property of some classes of sets in , Acta Univ. Carolin. Math. Phys. 39 (1998), no. 1-2, 111–118.
- ↑ Z. Gyenes, The ratio of the perimeter and the area of unions of copies of a fixed set, Discrete Comput. Geom. 45 (2011), no. 3, 400–409.
- ↑ Z. Gyenes, The ratio of the surface-area and volume of finite un ion of copies of a fixed set in , MSc thesis, 2005.
- ↑ Viktor Kiss, Zoltán Vidnyánszky. Unions of regular polygons with large perimeter-to-area ratio (англ.) // Discrete Comput. Geom.. — 2015. — Vol. 53. — P. 878—889. Архивировано 17 августа 2016 года.
Ссылки
[править | править код]- Pálvölgyi Dömötör, Is the ratio Perimeter/Area for a finite union of unit squares at most 4?, MathOverflow.
На эту статью не ссылаются другие статьи Википедии. |









