Древесная декомпозиция (:jyfyvugx ;ytkbhk[nenx)

Граф с восемью вершинами и его древесная декомпозиция в дерево с шестью узлами. Каждое ребро графа соединяет две вершины, перечисленные вместе в некотором узле дерева, и каждая вершина графа указана в узлах непрерывных поддеревьев дерева. Каждый узел дерева перечисляет максимум три вершины, так что ширина этого разложения равна двум.

В теории графов древесная декомпозиция — это отображение графа в дерево, которое может быть использовано для определения древесной ширины графа и ускорения решения определённых вычислительных задач на графах.

В области машинного обучения древесная декомпозиция называется также деревом сочленений, деревом клик или деревом смежности. Древесная декомпозиция играет важную роль в задачах, подобных вероятностному логическому выводу, поиску допустимых значений, оптимизации запросов СУБД и разложения матриц.

Понятие древесной декомпозиции было первоначально предложено Халином. Позднее его переоткрыли Робертсон и Сеймур и с тех пор понятие изучалось многими другими авторами.

Определение

Интуитивно древесная декомпозиция представляет вершины заданного графа G как поддеревья дерева таким образом, что вершины графа смежны только тогда, когда соответствующие поддеревья пересекаются. Тогда G образует подграф графа пересечений поддеревьев. Полный граф пересечений — это хордальный граф.

Каждое поддерево связывает вершину графа с множеством узлов дерева. Чтобы определить это формально, мы представим каждый узел дерева как множество вершин, связанных с ней. Тогда для заданного графа G = (V, E) древесная декомпозиция — это пара (X, T), где X = {X₁, ..., X_n} является семейством подмножеств множества V, а T является деревом, узлами которого служат подмножества X_i, удовлетворяющие следующим свойствам:

1. Объединение всех множеств X_i равно V. Таким образом, любая вершина графа связана хотя бы с одним узлом дерева.
2. Для любого ребра (v, w) графа существует подмножество X_i, содержащее как v, так и w. Таким образом, вершины смежны в графе, если только они соответствуют поддеревьям, имеющим общий узел.
3. Если X_i и X_j содержат вершину v, то все узлы X_k дерева в (уникальном) пути между X_i и X_j содержат v тоже. То есть узлы, связанные с вершиной v, образуют связное подмножество в T. Это свойство можно сформулировать эквивалентно — если $X_{i}$, $X_{j}$ и $X_{k}$ являются узлами, а $X_{k}$ находится на пути из $X_{i}$ в $X_{j}$, то $X_{i}\cap X_{j}\subseteq X_{k}$.

Древесная декомпозиция графа далеко не уникальна. Например, тривиальная древесная декомпозиция содержит все вершины графа в корневом узле.

Древесная декомпозиция, в которой деревом служит путь, называется путевой декомпозицией и древесная ширина этого специального вида древесной декомпозиции известна как путевая ширина.

Древесная декомпозиция (X, T = (I, F)) с древесной шириной k является гладкой, если для всех $i\in I:|X_{i}|=k+1$ и для всех $(i,j)\in F:|X_{i}\cap X_{j}|=k$.

Древесная ширина

Основная статья: Древесная ширина (теория графов)

Две различные древесные декомпозиции одного графа

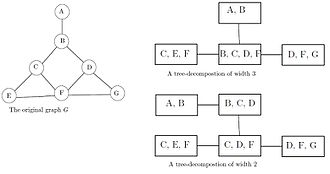
Ширина древесной декомпозиции — это размер её наибольшего множества X_i без единицы. Древесная ширина tw(G) графа G — это минимальная ширина среди всех возможных декомпозиций графа G. В этом определении размер наибольшего множества уменьшен на единицу с целью сделать древесную ширину дерева равной единице. Древесную ширину можно определить исходя из других структур, а не древесной декомпозиции. Сюда входят хордальные графы, ежевики и гавани.

Определение, не превосходит ли древесная ширина заданного графа G величину k, является NP-полной задачей . Однако, если k является фиксированной константой, граф с древесной шириной k может быть распознан и древесная декомпозиция ширины k может быть построена за линейное время. Время работы этого алгоритма зависит от k экспоненциально.

Динамическое программирование

В начале 1970-х было замечено, что задачи из большого класса комбинаторных оптимизационных задач на графах могут быть эффективно решены с помощью несериального динамического программирования, если граф имеет ограниченную размерность, связанный с древесной шириной параметр. Позднее некоторые авторы независимо обнаружили к концу 1980-х , что многие алгоритмические NP-полные задачи для произвольных графов могут быть эффективно решены с помощью динамического программирования для графов ограниченной древесной шириной при использовании древесной декомпозиции этих графов.

В качестве примера представим себе задачу поиска наибольшего независимого множества на графе с древесной шириной k. Для решения этой задачи сначала выберем один узел древесного разложения в качестве корня (произвольным образом). Для узла X_i древесной декомпозиции пусть D_i будет объединением множеств X_j, наследуемых от X_i. Для независимого множества S ⊂ X_i пусть A(S,i) означает размер наибольшего независимого подмножества I в D_i, такого, что I ∩ X_i = S. Подобным образом для смежной пары узлов X_i и X_j с X_i более дальним от корня по сравнению с X_j и независимого множества S ⊂ X_i ∩ X_j пусть B(S,i,j) означает размер наибольшего независимого подмножества I в D_i, такого, что I ∩ X_i ∩ X_j = S. Мы можем вычислить эти значения A и B проходом дерева снизу вверх:

$A(S,i)=|S|+\sum _{j}\left(B(S\cap X_{j},j,i)-|S\cap X_{j}|\right)$

$B(S,i,j)=\max _{S'\subset X_{i} \atop S=S'\cap X_{j}}A(S',i)$

Где сумма в формуле для $A(S,i)$ берётся по потомкам узла $X_{i}$.

В каждом узле или ребре имеется не более 2^k множеств S, для которых необходимо вычислить эти значения, так что в случае, когда k является константой, все вычисления занимают постоянное время на одно ребро или узел. Размер наибольшего независимого множества является наибольшим значением, запомненном в корневом узле, а само наибольшее независимое множество можно найти (что является стандартным для динамического программирования) путём отслеживания в обратном порядке этих запомненных значений, начиная с наибольшего значения. Таким образом, в графах ограниченной древесной ширины задача поиска наибольшего независимого множества может быть решена за линейное время. Подобные алгоритмы применимы для многих других задач на графах.

Такой подход с динамическим программированием применяется в области машинного обучения с помощью алгоритма дерева сочленений для распространения доверия на графах ограниченной древесной ширины. Подход также играет ключевую роль в алгоритмах вычисления древесной ширины и построения древесной декомпозиции. Как правило, такие алгоритмы имеют первый шаг, на котором аппроксимируется древесная ширина и строится древесная декомпозиция с этой приближённой шириной, а на втором шаге используется динамическое программирование на полученном древесном разложении с целью вычисления точного значения древесной ширины.

См. также

• Ежевика и гавань, два вида структур, которые можно использовать в качестве альтернативы древесной декомпозиции в определении древесной ширины графа
• Декомпозиция графа на ветви, тесно связанная структура, ширина которой линейно связана с древесной шириной
• Метод декомпозиции.