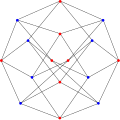
Граф Хоффмана (Ijgs }kssbgug)

Граф Хоффмана
Назван в честь	Алана Хоффмана
Вершин	16
Рёбер	32
Радиус	3
Диаметр	4
Обхват	4
Хроматическое число	2
Хроматический индекс	4
Свойства	Гамильтонов Двудольный Совершенный Эйлеров
Книжная толщина	3
Число очередей	2
Медиафайлы на Викискладе

Граф Хоффмана является 4-регулярным графом с 16 вершинами и 32 рёбрами, который открыл Алан Хоффман и опубликовал в 1963. Граф коспектрален графу гиперкуба Q₄.

Граф Хоффмана имеет много общих свойств с гиперкубом Q₄ — оба гамильтоновы и имеют хроматическое число 2, хроматический индекс 4, обхват 4 и диаметр 4. Граф также вершинно 4-связен и рёберно 4-связен. Однако радиус графа Хоффмана равен 3 в отличие от гиперкуба Q₄ (радиус которого равен 4). Граф Хоффмана не дистанционно-регулярен. Граф имеет книжную толщину 3 и число очередей 2.

Алгебраические свойства

Граф Хоффмана не вершинно-транзитивен и его полная группа автоморфизмов является группой порядка 48, изоморфной прямому произведению симметрической группы S₄ и циклической группы Z/2Z.

Характеристический многочлен графа Хоффмана равен

$(x-4)(x-2)^{4}x^{6}(x+2)^{4}(x+4)$,

что делает его целым графом — графом, спектр которого полностью состоит из целых чисел. Это тот же спектр, что и у гиперкуба Q₄.

Галерея

• 
  Граф Хоффмана гамильтонов.
• 
  Хроматическое число графа Хоффмана равно 2.
• 
  Хроматический индекс графа Хоффмана равен 4.