Головоломка «колючка» (Iklkfklkbtg «tklZctg»)

Головоломки «Колючки»

Головоломка «колючка» — головоломка сцепления, состоящая из брусков с выемками, комбинируя которые можно получить трёхмерную, обычно, симметричную, фигуру. Эти головоломки традиционно делаются из дерева, но можно найти и версии, сделанные из пластика или металла. Делаются «колючки» обычно с высокой точностью, чтобы обеспечить лёгкое скольжение и аккуратное совмещение частей. В последнее время определение «колючка» несколько расширилось и теперь не относится только к головоломкам, основанным на брусках.

Термин «колючка» впервые был упомянут в 1928 году Эдвином Уайеттом, но по тексту книги ясно, что термин широко использовался и до этого. Термин указывает на форму многих головоломок такого типа (в собранном виде), похожую на колючку.

Источники головоломок «колючки» неизвестны. Первая известная запись появилась в 1698 году как гравюра на титульном листе Циклопедии.. Более поздние упоминания можно найти в немецких каталогах конца XVIII и начала XIX веков. Существует мнение, что «колючки» изобрели китайцы, подобно другим классическим головоломкам, таким как танграм

«Колючка» из шести частей

Собранная колючка из шести частей

Колючка из шести частей, известная также как «Узел» или «Китайский крест», является наиболее известной и, по-видимому, старейшей головоломкой типа «колючка». На самом деле это семейство головоломок, имеющих одну и ту же форму в собранном виде и тот же базовый набор составляющих. Старейший патент США для головоломки этого рода датируется 1917 годом.

Многие годы «колючка» из шести частей была популярна, но была признана энтузиастами банальной и неинтересной. Большинство из сделанных и проданных головоломок были похожи одна на другую и большинство из них содержало «ключевую» деталь, брусок без выемок, который легко удалялся. В конце 1970-х годов, однако, «колючка» из шести частей вновь получила внимание изобретателей и коллекционеров, в основном благодаря компьютерному анализу, проведённому математиком Билом Катлером и его публикации в колонке Мартина Гарднера в Scientific American.

Структура

Все шесть частей головоломки являются квадратными брусками равной длины (которые по меньшей мере втрое длиннее ширины). В собранном виде бруски располагаются попарно в трёх перпендикулярных направлениях, взаимно пересекая друг друга. Выемки всех брусков располагаются в районе пересечения, так что в собранном виде выемки не видны. Все выемки можно описать как удаления кубиков (с ребром, равным половине ширины бруска), как показано на рисунке:

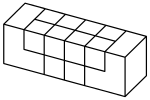
Имеется 12 возможных мест удаления кубиков и различные головоломки этого семейства сделаны из брусков с различным набором удалённых кубиков. Существует 4096 вариантов удаления кубиков. Из них мы удаляем приводящие к одинаковым брускам, в результате останется 837 возможных брусков. Теоретически из этих частей можно создать более 35 миллиардов возможных головоломок, однако число действительно головоломок оценивается менее чем в 6 миллиардов (то есть из которых можно действительно собрать фигуру).

Головоломка «Орех» из книги Хоффмана 1893 года в качестве примера сплошной «колючки»

Сплошные «колючки»

Головоломка «колючка» без внутренних пустот в собранном виде называется сплошной «колючкой». Головоломка может быть разобрана путём удаления бруска или группы брусков в один приём. До конца 1970-х годов сплошные «колючки» получали большую часть внимания и публикации относились только к этому типу. Число возможных сплошных «колючек» составляет 119 979 с использованием 369 видов брусков. Для всех этих головоломок требуется в общей сложности 485 деталей, поскольку некоторые головоломки используют одинаковые части.

«Колючка № 305», названная по её месту в таблице Катлера. Было найдено 314 наиболее «интересных» сплошных головоломок из брусков с пропилами, поскольку они не содержат одинаковых или симметричных частей, а также имеющих одно решение, не использующее ключ из 2 брусков

Типы брусков

По эстетическим, но большей частью по практическим, причинам бруски можно разделить на два типа:

• с пропилами — выемками, которые можно сделать пилой или фрезой.
• без пропилов — в которых внутренние углы могут быть сделаны с помощью стамески или путём склеивания частей.

Слева направо: с пропилами, без пропилов и брусок, технически, с пропилом, но его нельзя использовать с другими брусками с пропилами для создания сплошных «колючек»

59 брусков, которые можно использовать, имеют сквозные выемки, включая брусок вообще без выемок. Из них только 25 можно использовать для создания сплошных головоломок. Этот набор, часто называемый «25 брусков с пропилами», вместе с 17 дубликатами, можно использовать, чтобы собрать 221 вид различных «колючек». Некоторые из этих головоломок имеют более одного решения, давая в общей сложности 314 решений. Эти бруски очень популярны и их полный набор изготовляется и продаётся многими компаниями.

«Колючка Билла Баффлинга» пятого уровня (Билл Катлер)

Головоломка 7-го уровня израильского дизайнера Филиппе Дубоиса, продававшего свою головоломку под именем «Gaby Games»

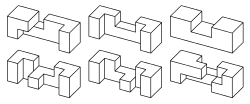
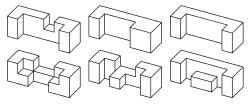
«Колючки» с пустотами

Для всех сплошных «колючек» одно движение требуется, чтобы удалить первый брусок или несколько брусков. «Колючка» с пустотами, имеющая внутренние полости в собранном состоянии, может потребовать более одного движения. Число движений, требуемых для удаления первого бруска, считается уровнем головоломки. Все сплошные «колючки», таким образом, имеют уровень 1. Чем выше уровень, тем сложнее головоломка.

В течение 1970—1980-х годов, эксперты пытались найти «колючки» с высшим уровнем. В 1979 году американский дизайнер и мастер Стюард Коффин нашёл головоломку 3-го уровня. В 1985 году Билл Катлер нашёл головоломку 5-го уровня, а вскоре была найдена головоломка 7-го уровня израильтянином Филиппе Дубоисом. В 1990 году Катлер завершил последнюю часть своего анализа и обнаружил, что высший уровень головоломок из брусков с пропилами равен 5, и что существует 139 таких головоломк. Высшим уровнем для «колючек» из шести брусков, имеющих более одного решения, является 12, что означает, что требуется сделать 12 движений, чтобы освободить первый брусок.

«Колючка» из трёх брусков

«Колючка» из трёх брусков

«Колючка» из трёх брусков, сделанная с «обычными» прямоугольными выемками (как в «колючках» из шести брусков), не может быть собрана или разобрана. Существуют, однако, некоторые «колючки» из трёх брусков с выемками другого вида. Наиболее известной головоломкой такого типа является упомянутая Уайеттом в книге 1928 года и состоящая из округлённых частей, которые нужно вращать.

Известные семейства «Колючек»

Головоломка Альтекрузе

Альтекрузе

Головоломка Альтекрузе названа по имени владельца патента 1890 года, хотя головоломка и существовала до этого. Фамилия «Altekruse» имеет австрийско-германское происхождение и означает на немецком «старый крест», что привело к подозрениям, что фамилия была псевдонимом, но человек с такой фамилией действительно эмигрировал в Америку в 1844 году вместе с тремя братьями, чтобы избежать призванными в прусскую армию, и есть подозрение, что это был один из заполнивших патент.

Классическая головоломка Альткрузе состоит из 12 одинаковых частей. Чтобы её разобрать, две половинки головоломки нужно двигать в противоположных направлениях. Если использовать ещё два таких же бруска, головоломку можно собрать другим способом. По тому же принципу можно собрать другие головоломки этого семейства с 6, 24, 36 и так далее частями. Несмотря на их размер, эти бо́льшие головоломки не считаются очень сложными, однако они требуют терпения и ловкости.

Головоломка «Чак»

Чак

Головоломка «Чак» разработана и запатентована Эдвардом Нельсоном в 1897. Дизайн был улучшен Роном Куком из британской компании Pentangle Puzzles, который разработал другие головоломки этого семейства

Головоломка «Чак» состоит, в основном, из U-образных частей различной длины, а некоторые имеют дополнительные выемки, которые используются как ключевые. Для создания больших глоловоломок (с названиями «Папа-Чак», «Дед-Чак» и «Прадедушка Чак») нужно добавить более длинные части. «Чак» можно считать расширением «колючки» из шести очень простых брусков, головоломки с названием «Дитя-Чак», которую очень легко решить. Части головоломки различной длины можно также использовать для создания несимметричных фигур, но собранных по тому же принципу, что и оригинальная головоломка.

Типичные части головоломки «Чак»: U-образные и ключевые

Пагода размера из 51 частей (изготовлена Филиппе Дубоисом)

Пагода

Истоки головоломки «Пагода», иногда называемой «Японским кристаллом», неизвестны. Головоломка упомянута в книге Уайетта 1928 года. Головоломки этого семейства можно рассматривать как расширение «колючки» из трёх брусков («Пагода» размера 1), однако головоломки не требуют специальных выемок. «Пагода» размера 2 состоит из 9 частей, а бо́льшие версии состоят из 19, 33, 51, и так далее частей. «Пагода» размера $n$ состоит из $2n^{2}+1$ частей.

Диагональные «колючки»

Диагональная «колючка» — головоломка «Гигантская звезда» (изготовитель — Gaya Games)

Хотя большинство головоломок «колючка» сделаны с квадратными выемками, некоторые сделаны с диагональными. Части диагональной «колючки» представляют собой квадратные бруски с вырезами в виде буквы V под углом 45°. Эти головоломки часто называют «Звёздами» и у брусков срезают рёбра под углом 45° по эстетическим причинам, что придаёт собранной головоломке звёздчатый вид.

См. также

• Верёвочные головоломки

Литература

• E. M. Wyatt. Puzzles in Wood. — Milwaukee, Wisc: Bruce Publishing Co, 1928. — ISBN 0-918036-09-7.
• Edwin Mather Wyatt. Puzzles in Wood. — 3rd. — Fox Chapel Publishing, 2007. — ISBN 1565233484.
• Jerry Slocum. New Findings on the History of the Six Piece Burr. — Slocum Puzzle Foundation, 1698.
• Jerry Slocum, Dieter Gebbardt. Puzzles from Catel's Cabinet and Bestelmeier's Magazine, 1785 to 1823. — Slocum Puzzle Foundation, 1997.
• Wei Zhang, Peter Rasmussen. Chinese Puzzles: Games for the Hands and Mind. — Art Media Resources, 2008. — ISBN 1588861015.
• Wei Zhang, Peter Rasmussen. Chinese Puzzles: Games for the Hands and Mind. — Art Media Resources, 2008. — ISBN 1588861015.
• Martin Gardner. Mathematical Games // Scientific American. — 1978. — С. 14–26.
• Stewart T. Coffin. Puzzle Craft. — 1992.
• William H. Cutler. The Six-Piece Burr // Journal of Recreational Mathematics. — 1978. — Т. 10, вып. 4. — С. 241–250.
• Professor Hoffmann. Chapter III, No. XXXVI // Puzzles old and new. — London: Frederick Warne and Co., 1893.
• A. K. Dewdney. Computer Recreations // Scientific American. — 1985. — Т. 253, вып. 4. — С. 16–27. — doi:10.1038/scientificamerican1085-16.
• Jerry Slocum, Dieter Gebbardt,. Puzzles from Catel's Cabinet and Bestelmeier's Magazine, 1785 to 1823. — Slocum Puzzle Foundation, 1997.
• Stewart Coffin. The Puzzling World of Polyhedral Dissections  (неопр.) (1998). Дата обращения: 7 ноября 2016. Архивировано 27 января 2017 года.
• Stewart T. Coffin. Geometric Puzzle Design. — Wellsley, K. Peters, 2007. — ISBN 1568813120.

Ссылки

• Ishino Keiichiro. Puzzle will be played...  (неопр.) Дата обращения: 19 февраля 2013. Архивировано 7 ноября 2016 года. На сайте описаны сотни головоломок «Колючка»
• Rob's Puzzle Page  (неопр.). Дата обращения: 7 ноября 2016. Архивировано 21 октября 2016 года.
• Things tagged with burr puzzle on Thingiverse  (неопр.). thingiverse. Дата обращения: 7 ноября 2016. Архивировано 27 сентября 2016 года.