Гиперболическая система координат (InhyjQklncyvtgx vnvmybg tkkj;nugm)

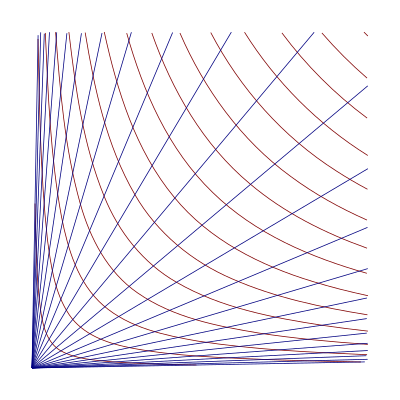
Гиперболическая система координат евклидовой плоскости. Все точки, принадлежащие одному и тому же синему лучу, имеют одинаковую координату u. Все точки, принадлежащие одной и той же красной гиперболе, имеют одинаковую координату v

Гиперболическая система координат в математике — система координат, позволяющая задать положение точек в первом квадранте Q декартовой плоскости.

$\{(x,y)\ :\ x>0,\ y>0\ \}=Q\ \!$.

Значения гиперболических координат принадлежат гиперболической плоскости, которая определяется так:

$HP=\{(u,v):u\in \mathbb {R} ,v>0\}$.

Данная система удобна для сравнения прямых пропорций из Q в логарифмической шкале и оценки отклонений от прямой пропорции.

Для $(x,y)$ в $Q$ примем

$u=\ln {\sqrt {\frac {x}{y}}}$

и

$v={\sqrt {xy}}$.

Параметр u представляет собой гиперболический угол к (x, y), в то время как v — среднее геометрическое x и y.

Обратное отображение:

$x=ve^{u},\quad y=ve^{-u}$.

Функция $Q\rightarrow HP$ непрерывна, но не является аналитической

Литература

• David Betounes (2001) Differential Equations: Theory and Applications, page 254, Springer-TELOS, ISBN 0-387-95140-7
• Scott Walter (1999). "The non-Euclidean style of Minkowskian relativity". Chapter 4 in: Jeremy J. Gray (ed.), The Symbolic Universe: Geometry and Physics 1890-1930, pp. 91–127. Oxford University Press. ISBN 0-19-850088-2