Гармоническая прогрессия (Igjbkuncyvtgx hjkijyvvnx)
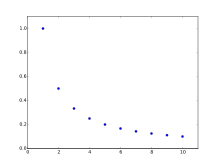
В математике гармоническая прогрессия (или гармоническая последовательность) — это прогрессия, образованная обратными элементами арифметической прогрессии.
Эквивалентное определение — это бесконечная последовательность вида
где a не равно нулю и −a/d не натуральное число, или конечная последовательность вида
где a≠0, k — натуральное число −a/d — не натуральное число или больше k.
Примеры
[править | править код]- 1, 1/2, 1/3, 1/4, 1/5, 1/6
- 12, 6, 4, 3, , 2, … , , …
- 30, −30, −10, −6, − , … ,
- 10, 30, −30, −10, −6, − , … ,
Сумма гармонической прогрессии
[править | править код]Бесконечные гармонические прогрессии не суммируемы (в смысле бесконечной суммы).
Для гармонической прогрессии невозможно при различных единицах дробей (кроме случаев с a = 1 и k = 0) иметь сумму, равную целому числу. Причина в том, что по крайней мере один знаменатель прогрессии будет делиться на натуральное число, на которое не делится любой другой знаменатель.[1]
Примечания
[править | править код]- ↑ Erdős, P. (1932), "Egy Kürschák-féle elemi számelméleti tétel általánosítása" [Generalization of an elementary number-theoretic theorem of Kürschák] (PDF), Mat. Fiz. Lapok (венг.), 39: 17—24, Архивировано (PDF) 6 мая 2021, Дата обращения: 22 ноября 2019 Источник. Дата обращения: 22 ноября 2019. Архивировано 6 мая 2021 года.. Цитата по Graham, Ronald L. [in английский] (2013), "Paul Erdős and Egyptian fractions", Erdős centennial, Bolyai Soc. Math. Stud., vol. 25, János Bolyai Math. Soc., Budapest, pp. 289—309, CiteSeerX 10.1.1.300.91, doi:10.1007/978-3-642-39286-3_9, ISBN 978-3-642-39285-6, MR 3203600.







