Биалгебра (>ngliyQjg)

Биалгебра — векторное пространство над полем, которое одновременно является унитальной ассоциативной алгеброй и коунитальной коассоциативной коалгеброй, так что алгебраическая и коалгебраическая структуры согласованы. А именно, коумножение и коединица являются гомоморфизмами унитальной алгебры, или, что эквивалентно, умножение и единица алгебры являются морфизмами коалгебры (эти утверждения эквивалентны, поскольку они выражаются одними и теми же коммутативными диаграммами).

Гомоморфизм биалгебр — это линейное отображение, которое является одновременно гомоморфизмом соответствующих алгебр и коалгебр. Из симметрии коммутативных диаграмм видно, что определение биалгебры является самодвойственным, поэтому, если возможно определить двойственное пространство к векторному пространству, на котором строится биалгебра (что всегда возможно, если оно конечномерно), то оно автоматически является биалгеброй.

Определение

Биалгеброй $(B,\nabla ,\eta ,\Delta ,\epsilon )$ с умножением $\nabla$, единицей $\eta$, коумножением $\Delta$ и коединицей $\epsilon$ над полем $K$ называется алгебраическая структура, обладающая следующими свойствами:

• $B$ является векторным пространством над полем $K$;
• заданы умножение, то есть линейное отображение $\nabla$: $B\otimes B\rightarrow B$ над полем $K$ (или, что эквивалентно, полилинейное отображение $\nabla$: $B\times B\rightarrow B$ над полем $K$) и единица, то есть линейное отображение $\eta$: $K\rightarrow B$, так что $(B,\nabla ,\eta )$ является унитальной ассоциативной алгеброй;
• заданы коумножение, то есть линейное отображение $\Delta$: $B\rightarrow B\otimes B$ над полем $K$, и коединица, то есть линейное отображение $\epsilon$: $B\rightarrow K$, так что $(B,\Delta ,\epsilon )$ является коунитальной коассоциативной коалгеброй;
• выполняются условия совместимости, выраженные следующими коммутативными диаграммами:

1. согласованы умножение $\nabla$ и коумножение $\Delta$

   

   где $\tau$: $B\otimes B\rightarrow B\otimes B$ является линейным отображением, определенным как $\tau (x\otimes y)=y\otimes x$ для всех $x$ и $y$ в $B$,

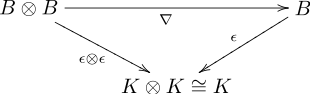
2. согласованы умножение $\nabla$ и коединица $\epsilon$

   

3. согласованы коумножение $\Delta$ и единица $\eta$

   

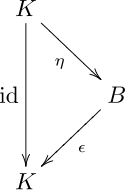
4. согласованы единица $\eta$ и коединица $\epsilon$

   

Ссылки

• Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001), Hopf Algebras: An introduction, Pure and Applied Mathematics, vol. 235 (1st ed.), Marcel Dekker, ISBN 0-8247-0481-9.