Алгоритм CDCL (Glikjnmb CDCL)

Алгоритм CDCL (англ. conflict-driven clause learning — «управляемое конфликтами обучение дизъюнктам») — основанный на алгоритме DPLL эффективный решатель (NP-полных) задач выполнимости булевых формул (SAT-решатель). Основная структура данных в CDCL-решателях — импликационный граф, фиксирующий назначения переменным, а другой особенностью является использование нехронологического возврата и запоминание дизъюнктов в ходе анализа конфликта.

Алгоритм был предложен Жуаном Маркесом-Сильвой (англ. João Marques-Silva) и Каремом Сакаллой (англ. Karem A. Sakallah) в 1996 году и независимо Роберто Байярдо (англ. Roberto J. Bayardo) и Робертом Шрагом (англ. Robert C. Schrag) в 1997 году.

Описание

DPLL-алгоритм, лежащий в основе CDCL-алгоритма, использует поиск с возвратом на конъюнктивных нормальных формах, на каждом шаге которого происходит выбор переменной и присвоения ей значения (0 или 1) для последующего ветвления, заключающегося в присваивании значения переменной, после чего упрощённая формула проходит рекурсивную проверку на выполнимость. В случае, когда встречается конфликт, то есть, полученная формула является невыполнимой, включается механизм возврата (бэктрекинга), при котором отменяются ветвления, в которых для переменной были опробованы оба значения. Если поиск возвращается к ветвлению первого уровня, вся формула объявляется невыполнимой. Такой возврат, свойственный алгоритму DPLL, называется хронологическим.

Дизъюнкты, используемые в алгоритме, делятся на выполнимые (satisfied), когда среди входящих в дизъюнкт значений есть 1, невыполнимые (unsatisfied) — все значения нулевые, единичные (unit) — все нули, кроме одной переменной, которой значение ещё не присвоено, и неразрешённые (unresolved) — все остальные. Одной из важнейших составляющих SAT-решателей является правило единичного дизъюнкта, при котором выбор переменной и её значения однозначен. (Следует напомнить, что в дизъюнкт входят как переменные, так и их отрицания.) Процедура распространения переменной (англ. unit propagation) (в современных CDCL-решателях она почти всегда основывается на правиле единичного дизъюнкта) производится после ветвления для вычисления логических следствий сделанного выбора.

В дополнение к DPLL и его механизму поиска с возвратом, CDCL использует некоторые другие приёмы:

• запоминание новых дизъюнктов в ходе поиска с возвратом.
• использование структуры конфликтов для получения и запоминания новых дизъюнктов.
• применение ленивых структур данных для представления формул.
• эвристики ветвления имеют низкие затраты вычислительных ресурсов и получают обратную связь от поиска с возвратами.
• периодический перезапуск поиска с возвратами.
• политики удаления для выученных дизъюнктов.
• другие виды оптимизации.

Схема алгоритма

С каждой переменной проверяемой на выполнимость формулы в CDCL-алгоритме связаны несколько вспомогательных значений:

• значение переменных ν(v_i)∈{0,u,1} для всех переменных v_i, где u служит для обозначения ещё не назначенной переменной
• уровень решения, на котором переменной было присвоено значение от −1 (не присвоено) до количества переменных.
• предпосылка (antecendent) — единичный дизъюнкт формулы, на основе которого последовало значение переменной по правилу единичного дизъюнкта. Для ещё неназначенных переменных и переменных, по которым было принято решение, имеет значение None.

Схематично типичный CDCL-алгоритм можно представить следующим образом:

   Алгоритм CDCL(φ, ν)
   вход: 
     φ - формула (КНФ)
     ν - отображение значений переменных в виде множества пар
   выход:
     SAT (формула выполнима) или UNSAT (невыполнима)
   если UnitPropagationConflict(φ, ν)
   то 
     возврат UNSAT
   L := 0                                    -- уровень решения
   пока NotAllVariablesAssigned(φ, ν)
     (x, v) := PickBranchingVariable(φ, ν)   -- принятие решения
     L := L + 1
     ν := ν ∪ {(x, v)}
     если UnitPropagationConflict(φ, ν)      -- вывод последствий
     то
       β := ConflictAnalysis(φ, ν)           -- диагностика конфликта
       если β < 0
       то
         возврат UNSAT
       иначе
         Backtrack(φ, ν, β)                  -- возврат (бэктрекинг)
         L := β
   возврат SAT

В этом алгоритме использовано несколько подпрограмм, которые помимо возврата значений могут изменять и переданные им по ссылке переменные φ, ν:

• UnitPropagationConflict итеративно применяет правило единичного дизъюнкта, возвращая значение Истина в случае нахождения невыполнимого дизъюнкта.
• NotAllVariablesAssigned проверяет, есть ли ещё неназначенные переменные.
• PickBranchingVariable выбирает переменную и назначаемое значение (1 или 0).
• ConflictAnalysis анализирует возникший конфликт, запоминает новый дизъюнкт и даёт уровень решения, к которому необходимо вернуться.
• Backtrack производит возврат к уровню, вычисленному в ходе анализа конфликта.

Процедура анализа конфликта является центральной для CDCL алгоритма.

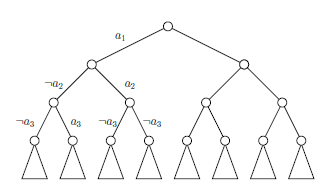
Основной структурой данных, используемой в CDCL-решателях, является импликационный граф (англ. implication graph), фиксирующий назначения переменным (как в результате решений, так и применением правила единичного дизъюнкта), в котором вершины соответствуют литералам формулы, а дуги фиксируют структуру импликаций.

Анализ конфликта

Процедура анализа конфликта (см. схему алгоритма) вызывается при обнаружении конфликта по правилу единичного дизъюнкта, и на её основе пополняется множество запомненных дизъюнктов. Процедура начинает с узла импликационного графа, в котором обнаружен конфликт, и охватывает уровни решения с меньшими номерами, переходя назад по импликациям пока не встречает самую свежую назначенную (в результате решения) переменную. Запомненные дизъюнкты применяются в нехронологическом возврате (англ. non-chronological backtracking) — ещё одном характерном для CDCL-решателей приёме.

Для сравнения:

• 
  DPLL: нет запоминания дизъюнктов, хронологический возврат.
• 
  CDCL: запоминание дизъюнктов в результате анализа конфликтов и нехронологический возврат

Идея использования структуры импликаций, приведших к конфликту, была развита в сторону применения UIP (англ. Unit Implication Points — «точки единичной импликации»). UIP — это доминатор импликационного графа, который у этого вида графа можно вычислить за линейное время. UIP представляет собой альтернативный вариант назначения переменных и дизъюнкт, запомненный в первой такой точке, гарантированно имеет наименьший размер и обеспечивает наибольшее уменьшение уровня решения. В связи с применением эффективных ленивых структур данных, авторы многих SAT-решателей, например, Chaff, применяют метод первого UIP для запоминания дизъюнктов (англ. first UIP clause learning).

Корректность и полнота

Как и DPLL, алгоритм CDCL является корректным и полным SAT-решателем. Так, запоминание дизъюнктов не влияет на полноту и корректность, так как каждый запомненный дизъюнкт может быть выведен из начальных дизъюнктов и других запомненных дизъюнктов методом резолюции. Изменённый механизм возврата также не влияет на полноту и корректность, так как информация о возврате сохраняется в запомненном дизъюнкте.

Пример

Иллюстрация работы алгоритма:

• 
  Выбор переменной для ветвления: x1. Жёлтый кружок означает произвольное решение.
• 
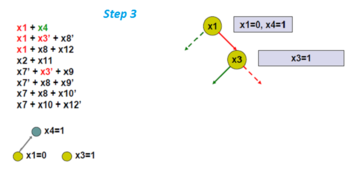
  По правилу единичного дизъюнкта x4 должно быть 1. Серый кружок — принудительное назначение. Получаемый граф и есть импликационный граф.
• 
  Произвольный выбор другой переменной, x3.
• 
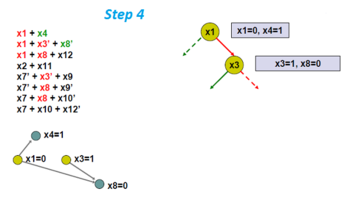
  Применение правила единичного дизъюнкта и нахождение нового импликационного графа.
• 
  Переменные x8 и x12 с логической необходимостью принимают значения 0 и 1 соответственно.
• 
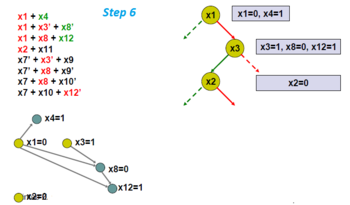
  Снова выбор переменной ветвления: x2.
• 
  Построение импликационного графа.
• 
  Ещё одна переменная: x7.
• 
  Построение импликационного графа.
• 
  Новый импликационный граф. Получен конфликт.
• 
  Нахождение разреза графа, приведшего к конфликту, и конфликтного дизъюнкта.
• 
  Нахождение дизъюнкта по отрицанию: если из a следует b, то из не-b следует не-a
• 
  Запоминание дизъюнкта.
• 
  Нехронологический возврат на соответствующий уровень решения.
• 
  Соответствующие установки значений.

Применения

SAT-решатели на основе CDCL-алгоритма находят применение в автоматическом доказательстве теорем, криптографии, проверке моделей и тестировании аппаратного и программного обеспечения, биоинформатике, определении зависимостей в системах управления пакетами и т. п.

Литература

• Armin Biere, Marijn Heule, Hans van Maaren and Toby Walsch. Chapter 4. Conflict-Driven Clause Learning SAT Solvers // Handbook of Satisfiability. — IOS Press, 2008.
• Matthew W. Moskewicz; Conor F. Madigan; Ying Zhao; Lintao Zhang; Sharad Malik (2001). "Chaff: Engineering an Efficient SAT Solver". Annual ACM IEEE Design Automation Conference. pp. 530–535.{{cite conference}}: Википедия:Обслуживание CS1 (множественные имена: authors list) (ссылка)
• Hamadi, Y. Combinatorial Search: From Algorithms to Systems. — Springer Berlin Heidelberg, 2013. — 152 p. — ISBN 9783642414824.
• Audemard, Gilles; Bordeaux, Lucas; Hamadi, Youssef; Jabbour, Saïd; Sais, Lakhdar. A Generalized Framework for Conflict Analysis. — В: Lecture Notes in Computer Science // SAT. — Springer, 2008. — 21-27 с.
• Pradhan, D.K. and Harris, I.G. Practical Design Verification. — Cambridge University Press, 2009. — P. 252-254. — ISBN 9780521859721.
• Järvisalo, M.; Van Gelder, A. Theory and Applications of Satisfiability Testing. — SAT 2013: 16th International Conference, Helsinki, Finland, July 8-12, 2013. Proceedings. — Springer Berlin Heidelberg, 2013. — ISBN 9783642390715.

Ссылки

• Marques-Silva & Mikolas Janota. CDCL SAT Solvers & SAT-Based Problem Solving  (неопр.). SAT/SMT Summer School 2013, Aalto University, Espoo, Finland. (недоступная ссылка)
• Masahiro Sakai. How a CDCL SAT solver works (англ.) (2012).